Quizá no sea familiar para ti y te preguntes ¿qué es esto de la conversión de coordenadas en el plano? Pues sí, existen dos tipos de coordenadas en el plano, y es posible convertir unas en otras.
Ya aprendimos acerca de esto en un post anterior al que te dejo vínculo aquí: Tipos de coordenadas en el plano. Al finalizar el mismo, dejamos planteado que dedicaríamos este post a compartir dos ejemplos de cómo hacer esta conversión. En primer término veremos cómo hacer conversión de coordenadas cartesianas a coordenadas polares; en el segundo caso veremos la situación inversa, es decir, de polares a cartesianas.
Veamos entonces esos ejemplos que nos enseñarán sobre…
Conversión de coordenadas en el plano
- Primer caso
Tenemos la ubicación un punto expresado en coordenadas cartesianas (x,y) y necesitamos expresar sus referencias con coordenadas polares (r,θ).
Para hacerlo, hemos de constituir un triángulo rectángulo, del cual en los hechos conoces los dos catetos, que están dados por la coordenada “x” y la coordenada “y”. El reto consiste en resolverlo, es decir hallar “r”, que hallar la hipotenusa del triángulo. Acto seguido, debemos calcular el ángulo θ, lo que puede hacerse a través de alguna de las funciones trigonométricas más usuales, por ejemplo, podría ser la tangente, pues conoces los catetos, que en este caso son las coordenadas antes señaladas.
Veamos este caso:
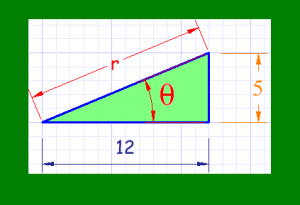Se trata de expresar el punto (12,5) en coordenadas polares.
Para calcular “r”, nos valemos del Teorema de Pitágoras, porque en definitiva el lado que falta es ni más ni menos la hipotenusa del triángulo rectángulo en cuestión. Ha aquí la solución:
r2 = 122 + 52
r = √ (122 + 52)
r = √ (144 + 25) = √ (169) = 13
Una vez calculado “r”, utilizamos la función tangente para calcular el ángulo en cuestión, vale decir el parámetro que nos falta para completar las coordenadas polares. Procedemos así:
tan( θ ) = 5 / 12
θ = atan( 5 / 12 ) = 22.6°
- Segundo caso
Estamos hablando del caso inverso, es decir cuando la ubicación de un punto se ha expresado en función de coordenadas polares, y queremos expresarla en coordenadas cartesianas. En definitiva nos valdremos del mismo recurso, utilizaremos funciones trigonométricas. En este caso, el reto es resolver un triángulo rectángulo del que se te han dado un ángulo y la longitud de su hipotenusa
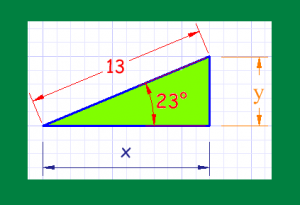
Veamos cómo proceder, por ejemplo en el caso de que las coordenadas polares sean (13, 23 °). La siguiente figura nos ayuda a analizar el caso en cuestión:
Los pasos a seguir serían en este caso, los siguientes:
1) Nos valdremos de la función coseno para hallar x, y el cálculo que estamos planteando será el siguiente:
cos( 23 °) = x / 13
Despejamos la incógnita x, y nos queda:
x = 13 × cos( 23 °)
x = 13 × 0.921
x = 11.98
2) Nos valdremos de la función seno para hallar la coordenada y. El planteo que realizamos en este caso, es:
sen( 23 °) = y / 13
Despejamos la incógnita, y planteamos:
y = 13 × sin( 23 °)
y = 13 × 0.391
y = 5.08
Te invito a estar pendiente, pues en los próximos días compartiremos un ejercicio test para que puedas evaluar y practicar acerca de estas conversiones.
Imagen: es.wikipedia
