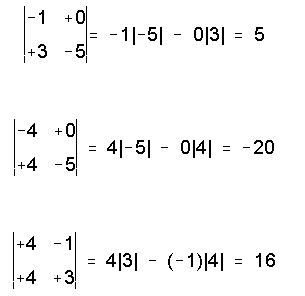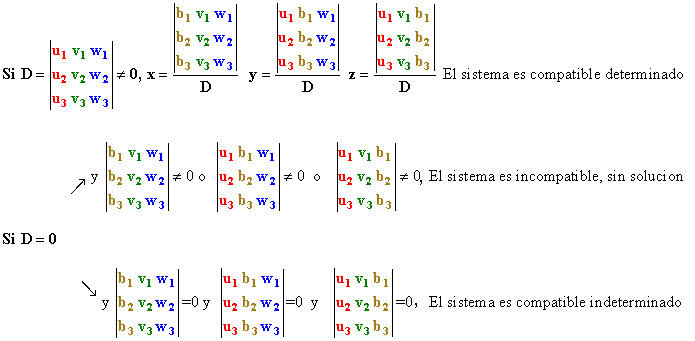Un determinante es el valor asociado a una matriz y solo se puede sacar a una matriz cuadrada.
Existen distintos métodos para poder sacar los determinantes a las matrices repasaremos los mas comunes.
1) Metodo de Cofactores
Consiste en los siguientes pasos:
- Escoger una fila o una columna.
- Para cada término de la fila o columna, llamados cofactors, quitamos la fila o columna en la que esta y lo que queda es el menor.
- Multiplicar el valor del menor por el cofactor y por su signo y sumar lo de todos los cofactores.
Para saber el signo de los factores es necesario tener en cuenta el signo que les corresponde por el hecho de su posición, para conocer esto siempre hay que tener en cuenta la siguiente matriz de signos:
[+ – + – …]
[- + – + …]
[+ – + – …]
[- + – + …]
…
Y así sucesivamente es como varia la matriz de signos entonces a la hora de realizar el método es necesario aplicar el signo que le corresponde a cada numero en la operación que se realice.
Para hacer mas gráfico este método aquí esta con una matriz de 2×2
[a11 a12]
[a21 a22]
+(a11)(a22) + (a12)(-a21) = a11a22 – a12a21
1) 1er fila
2) Para a11 su menor es a22 y su signo es +. Para a12 su menor es a21 y su signo es -.
Una pequeña nota para este método, para matrices de 2×2 su determinante es la resta de sus productos cruzados, ya para matrices mayores si se hace el método de cofactores.
Aquí unos ejemplos para este método:
- [4 -3]
[5 7]
Siguiendo el método de cofactores y nuestro pequeño asterisco para las matrices de 2×2 tenemos
Det = 4×7 + -3(-)(5) = 28 + +15 = 43
- [1/3 4/7]
[-2/9 7/5]
Det = 1/3(7/5) + -(4/7)(-2/9) = 4/15 + +8/63 = 89/315
- [3 5 2]
[4 2 3]
[-1 2 4]
Ahora tenemos el caso de una matriz de 3×3, aquí si hay que aplicar el método de cofactores, entonces escogemos una fila o columna y a raíz de esta empezamos a aplicar:
3 [2 3] = 3 [(2)(4) + -(3)-(2)] = 3[8 – 6]= 2
[2 4]
-5 [4 3] = -5[4(4) + -3(-1)] = -5[19]= -95
[-1 4]
2 [4 2] = 2[4(2) + -2(-1)] = 2[8+2]=20
[-1 2]
Para calcular el determinante final lo único que tenemos que hacer es sumar el resultado de los determinantes obtenidos y listo. Por lo que el determinante de nuestra matriz original nos queda:
Det= -69
Este método aplica a cualquier matriz de cualquier tamaño sin excepción alguna, para 2×2 solo se necesita sumar los productos cruzados y para estos cuando los 4 son positivos al primero se le restara el segundo producto cruzado y cuando dentro 2do del R1 o el 1ro del R2 son negativos se sumaran ambos productos cruzados.
El método de cofactores es el mas común y con el se pueden resolver todas las matrices de cualquier tamaño, pero como veremos también existe otro muy particular para un especifico tamaño de matrices y ese es:
2) Metodo único para matrices de 3×3:
Este metodo consiste en:
- Aumentar a la derecha las dos primeras columnas o abajo las dos primeras filas de tal manera que con estas obtengamos la multiplicación de las diagonales principales y sumar sus productos de cada una y restar de este valor la suma de las multiplicaciones de las otras diagonales.
Aqui un ejemplo:
1. Sacar el determinante a la siguiente matriz:
[3 5 2]
[4 2 3]
[-1 2 4]
Como dice la instrucción del método lo primero que tenemos que haces es elegir entre las dos primeras columnas o las dos primeras filas, ya depende de cada uno, para este ejemplo utilizaremos las dos primeras columnas.
Entonces tenemos:
[3 5 2] 3 5
[4 2 3] 4 2
[-1 2 4] -1 2
Ahora multiplicamos sus diagonals principales y los sumamos y le restamos la multiplicación de las otras diagonales, entonces:
Det = [(3x2x4) + (5x3x-1) + (2x4x2)] – [(-1x2x2) + (2x3x3) + (4x4x5)]
Det = [25-15+16] – [-4 +18+180] = 25-94
Det = -69
Esta fue la matriz anterior que resolvimos por Cofactores para que también veamos que se puede por este otro método y que a algunos les resultara mas sencillo.
Otro ejemplo para aclarar dudas respecto al método:
2. Sacar el determinante a la siguiente matriz:
[3 2 0]
[0 4 -2]
[0 0 7]
Añadimos las dos primeras columnas a nuestra matriz
[3 2 0] 3 2
[0 4 -2] 0 4
[0 0 7] 0 7
Ahora multiplicamos las primeras diagonales y restamos las otras diagonales
Det = [12×7 + 0 + 0] – [0 + 0 +0] = 84 – 0
Det = 84
Esta es la manera ams sencilla de resolver matrices de 3×3, la forma mas sencilla de resolver seria con las dos primeras columnas ya que es mas gráfica la multiplicación para encontrar cualquier error algebraico cometido.
Estos son los métodos para encontrar los determinantes de las matrices cuadradas, son sencillos y cada uno tiene su forma de hacerlo.
Mas ejercicios:
Encontrar los determinantes de las siguientes matrices:
[1 0 3]
[0 1 4]
[2 1 0]
2.
[10 10 -8]
[-7 0 -2]
[10 6 9]
3.
[-2 10]
[0 5]
4.
[7 4]
[-1 10]