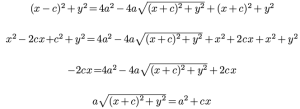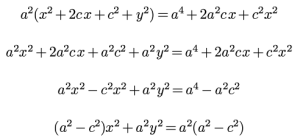 Se llama elipse al lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos F y F’ es una cantidad constante, que se representa por 2a. Así, para cualquier punto M de la curva, se tiene MF + MF’ = 2a. Ahora veremos como encontrar la ecuación de la elipse.
Se llama elipse al lugar geométrico de los puntos de un plano cuya suma de distancias a dos puntos fijos F y F’ es una cantidad constante, que se representa por 2a. Así, para cualquier punto M de la curva, se tiene MF + MF’ = 2a. Ahora veremos como encontrar la ecuación de la elipse.
Elementos de la elipse
- Los puntos fijos F y F’ se llaman focos y la longitud FF’ distancia focal que se designa por 2c.
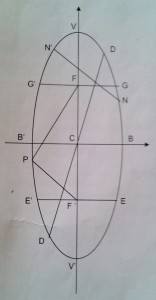
- El punto medio de FF’ es el centro de la elipse y se representa por C.
- Los segmentos PF y PF’ que une un punto cualquiera de la elipse con los focos se llaman radios.
- Un segmento que une dos puntos MN’ cualesquiera de la elipse se denomina cuerda.
- Una cuerda que pasa por el centro, tal como DD’, es un diámetro.
- El diámetro que pasa por los focos se llama eje mayor, o focal VV’, que se designa por 2a y el perpendicular a él es el eje menor o normal BB’, que se designa por 2b.
- Las intersecciones V, V’ y B, B’ de la elipse con los ejes son los vértices de las elipse.
- Las cuerdas EE’ y GG’ que pasan por los focos y son perpendiculares al eje mayor son los lados rectos de la elipse.
- Excentricidad de una elipse es la razón de la semidistancia focal al semieje mayor (c/a) y se prepresenta por e. paara que sea elipse c < a.
Propiedades de la elipse
- El eje mayor es igual a la cantidad constante VV’ = 2a
- El eje menor es igual BB’ = 2b
- La distancia focal FF’ = 2c
- Los ejes se cortan en su punto medio C
- El cuadrado del semieje mayor es igual a la suma de los cuadrados del semieje menor y de la semidistancia focal. \begin{align} a^{2} =b^{2} +c^{2} \end{align}
- La excentricidad es siempre menor que 1.
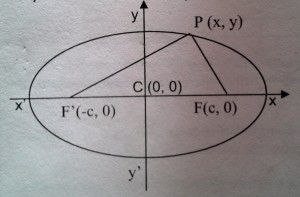
Ecuación de la elipse de C (o,0) y eje focal sobre el eje “x”
 \begin{align} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =1 \end{align}
\begin{align} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =1 \end{align}
Demostración
1. La propiedad que caracteriza a los puntos de la elipse es:
\begin{align} {PF} + {PF}’ = 2a \end{align}
2. Las coordenadas de F son (c,0) y las de F’ (-c,o) y las longitudes de MF y MF’ son:
\begin{align}{PF} = \sqrt{( x-c )^{2} +y^{2} }\end{align}
\begin{align}{PF}’ = \sqrt{( x+c )^{2} +y^{2}}\end{align}
3. Expresando analíticamente la igualdad:
\begin{align} \sqrt{( x-c )^{2} +y^{2} } + \sqrt{( x+c )^{2} +y^{2}} = 2a\end{align}
4.Transformando. Aislando el primer radical en el primer miembro, elevando al cuadrado:
5. Haciendo operaciones y reduciendo queda:
6. Elevando nuevamente al cuadrado:
7. De la propiedad 5 se deduce:
\begin{align} b^{2} x^{2} +a^{2} y^{2} =a^{2} b^{2} \end{align}
8. Dividiendo entre a2b2 resulta la ecuación de la elipse:
\begin{align} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =1 \end{align}
Ecuación de la elipse de C (o,0) y eje focal sobre el eje “y”
\begin{align}\frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} =1 \end{align}
Nota: la demostración se realiza de manera similar a la del eje de las “x”, solo cambia las coordenadas de los focos a (0,c) y (0,-c).
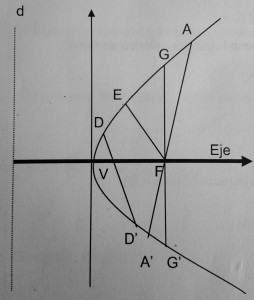
Pasos para graficar una ecuación de la elipse
- Ubicamos en el plano centro, vértices y focos.
- Ponemos dos puntos M que estén entre el centro y el foco.
- Abrimos el compás del vértice más cercano al primer punto M
- Nos paramos sobre el foco (para ambos focos) y hacemos un corte de cada lado sin cruzar ejes.
- Abrimos el compás del vértice más lejano al mismo punto M.
- Nos paramos sobre el foco y cortamos los trazos hechos previamente. NOTA: si los trazos son demasiado grandes es preferible borrar lo innecesario.
- Repetimos con M2
- Marcamos los puntos de cruce y unimos con los vértices.
Formulario para la elipse con centro c (0,0)
|
Fórmula de: |
Eje mayor “x” |
Eje mayor “y” |
|
Ecuación de la elipse |
\begin{align} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} =1 \end{align} |
\begin{align}\frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} =1 \end{align} |
|
Focos |
F(c,0) F’(-c,0) |
F(0,c) F’(0,-c) |
|
Vértices del eje mayor |
V(a,0) V’(-a,0) |
V(0,a) V’(0,-a) |
|
Vértices del eje menor |
B(0,b) B’(0,-b) |
B(b,0) B’(-b,0) |
|
Longitud del eje mayor |
VV’=2a |
VV’=2a |
|
Longitud del eje menor |
BB’=2b |
BB’=2b |
|
Distancia focal |
FF’=2c |
FF’=2c |
|
Excentricidad |
e=c/a |
e=c/a |
|
Longitud del lado recto |
LR = 2b2/a |
LR = 2b2/a |
|
Relación pitagórica |
\begin{align} a^{2} =b^{2} +c^{2} \end{align} |
\begin{align} a^{2} =b^{2} +c^{2} \end{align} |