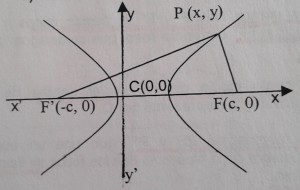
Para obtener la ecuación de la hipérbola hay que definir que es una hipérbola, esta es el lugar geométrico de los puntos de un plano cuya diferencia de distancias a dos puntos fijos F y F’ es una cantidad constante que se representa por 2a. Así para cualquier punto P de la curva, se tiene PF – PF’ = 2a.
Elementos de la hipérbola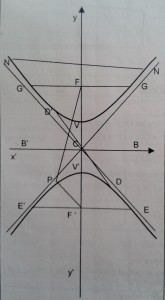
- La curva es abierta y consta de dos ramas.
- Los puntos fijos F y F’ se llaman focos y la longitud FF’ distancia focal que se designa por 2c.
- El punto medio de FF’ es el centro de la hipérbola (c).
- Los segmentos PF y PF’ que unen un punto cualquiera de la hipérbola con los focos se llaman radios.
- Un segmento que une dos puntos NN’ cualesquiera de la hipérbola se denomina cuerda.
- Una cuerda que pasa por el centro, como DD’ se llama diámetro.
- El diámetro que pasa por los focos se llama eje real, focal o transverso VV’ que se designa por 2a. Sobre la recta perpendicular al eje focal, que pasa por el centro O y que no corta a la curva, se considera un segmento BB’, llamado eje conjugado o imaginario que se designa por 2b.
- Las intersecciones V, V’ del eje focal con la curva son los vértices de la hipérbola.
- Las cuerdas EE’ y GG’ que pasan por los focos y son perpendiculares al eje mayor son los lados rectos de la hipérbola.
- Excentricidad de una elipse es la razón de la semidistancia focal al semieje mayor (c/a) y se representa por e. Para que sea hipérbola c>a.
- La curva está comprendida dentro del ángulo formado por las diagonales del rectángulo, cuyas dimensiones son 2a y 2b. Estas rectas se llaman asíntotas.
Propiedades de la hipérbola
- El eje real es igual a la cantidad constante VV’ =2a
- El eje conjugado es igual a BB’ = 2b
- La distancia focal FF’ =2x
- Los ejes se cortan en su punto medio c.
- Relación entre los semiejes y la semidistancia focal el: \begin{align}c^{2} =a^{2} +b^{2}\end{align}
- La excentricidad siempre es mayor que 1.
Ecuación de la hipérbola con c(0,0) y eje focal sobre el eje “x”
\begin{align}\frac{x^{2}}{a^{2}} – \frac{y^{2}}{b^{2}} =1\end{align}
Ecuación de la hipérbola con c(0,0) y eje focal sobre el eje “y”
\begin{align}\frac{y^{2}}{a^{2}} – \frac{x^{2}}{b^{2}} =1\end{align}
Pasos para graficar la ecuación de la hipérbola
- Ubicar todos los puntos importantes.
- Hacemos un rectángulo que pase por los cuatro vértices.
- Hacemos las diagonales y las prolongamos. Es decir las asíntotas.
- Poner un punto M después del foco.
- Abrimos el compás de M al vértice más cercano.
- Nos paramos en el foco y hacemos trazos sin cortar ninguna linea.
- Abrimos el compás e M al vértice más lejano.
- Nos paramos en el foco y cortamos guiandonos con x.
- Unimos los puntos.
Formulario para la hipérbola con centro (0,0)
|
Formula de: |
Eje transverso “x” |
Eje transverso “y” |
|
Ecuación de la hipérbola |
\begin{align}\frac{x^{2}}{a^{2}} – \frac{y^{2}}{b^{2}} =1\end{align} |
\begin{align}\frac{y^{2}}{a^{2}} – \frac{x^{2}}{b^{2}} =1\end{align} |
|
Focos |
F(c,0) F’(-c,0) |
F(0,c) F’(0,-c) |
|
Vértices |
V(a,0) V’(-a,0) |
V(0,a) V’(0,-a) |
|
Extremos del eje conjugado |
B(0,b) B’(0,-b) |
B(b,0) B’(-b,0) |
|
Longitud del eje real o transverso |
VV’=2a |
VV’=2a |
|
Longitud del eje imaginario o conjugado |
BB’=2b |
BB’=2b |
|
Distancia focal |
FF’=2c |
FF’=2c |
|
Excentricidad |
e=c/a |
e=c/a |
|
Longitud del lado recto |
\begin{align} {LR} = \frac{2b^{2}}{a}\end{align} |
\begin{align} {LR} = \frac{2b^{2}}{a}\end{align} |
|
Relación pitagórica |
\begin{align}c^{2} =a^{2} +b^{2}\end{align} |
\begin{align}c^{2} =a^{2} +b^{2}\end{align} |
|
Ecuaciones de las asíntotas |
bx+ay= 0 y bx-ay=0 |
ax+by= 0 y ax-by=0 |