El tema de hoy es ecuaciones simultáneas, método gráfico. Estamos trabajando para resolver ecuaciones simultáneas de primer grado y este es el cuarto método que estamos aprendiendo.
Si quieres repasar o practicar los que vimos anteriormente, aquí mismo te dejo vínculo al primero de los métodos algebraicos que vimos, el método de igualación , al segundo el método de sustitución, y al tercero, el método de reducción.
Ecuaciones simultáneas, método gráfico
Te presento el sistema que resolveremos para enseñarte como siempre a través de un ejemplo y comentando cada paso que vamos dando.
He elegido un sistema sencillo, que consta de dos ecuaciones simultáneas sin coeficientes, para que los pasos que voy citando y realizando a continuación sean más sencillos de hacer y comprender. Presta atención y al final te reitero a modo de resumen, la lista de pasos que debes hacer para resolver.
1) Convierte cada una de las ecuaciones del sistema en una función lineal. Esto se hace sencillamente despejando la incógnita “y”, que quedará en función de la x. En el caso del sistema que estamos trabajando como ejemplo nos quedará así:
Las funciones que utilizaremos son las que están recuadradas.
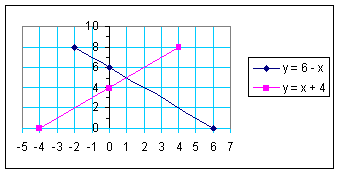
2) Elige una de ellas y construye una tabla de valores para hallar las coordenadas que luego volcarás en la gráfica. Como se trata de funciones lineales, es suficiente con que halles dos valores para cada caso (ya que necesitas sólo dos puntos para definir una recta), pero te recomiendo que hagas algún valor más, teniendo en cuenta que todas las coordenadas deberán pertenecer a la misma recta al momento de graficar. Si algún par de coordenadas no corresponde, revisa tus cálculos porque tal vez hayas cometido un error.
3) En un sistema de ejes coordenados cartesianos, representa con diferentes colores, las rectas que corresponden a cada función, teniendo en cuenta que cada par de valores que has calculado corresponde a las coordenadas de cada punto.
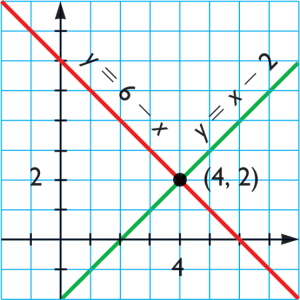
Para el caso de nuestro ejemplo, esta representación gráfica quedará de esta forma.
4) Observa cuál es el punto de corte de ambas rectas, esto es muy importante, porque las coordenadas de ese punto de corte son las soluciones del sistema de ecuaciones simultáneas. En el caso de este ejemplo se nota claramente que las coordenadas del punto de corte son las siguientes:
x=1
y=5
Precisamente esas son las soluciones de las ecuaciones simultáneas.
5) Verifica los valores hallados en el sistema de ecuaciones simultáneas original. Como en toda verificación, las igualdades deben cumplirse.
En el caso del sistema ejemplo con el que estamos trabajando, esta es la verificación que debes realizar:
1) x + y = 6
1 +5 =6
6=6
2)
x – y= -4
1 -(5)= -4
-4 = -4
A los efectos de resumir los pasos que debes seguir para utilizar este método de resolución de ecuaciones simultáneas de primer grado, sintetizo tal como te prometí lo que debes realizar:
- 1) Convierte ambas ecuaciones en funciones lineales
- 2) Realiza una tabla de valores por separado para cada una
- 3) Representa gráficamente cada recta en color diferente para cada ecuación
- 4) Las rectas debería cortarse; las coordenadas del punto de corte son las soluciones “x=…” e “y=…” que estás buscando.
- 5) Verifica los resultados encontrados en las ecuaciones simultáneas originales.

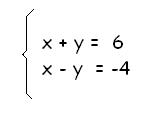







GRACIAS! El unico sitio en donde pude comprender el metodo grafico para resolver sistemas de ecuaciones de dos incognitas 😀
Hola Rossana! Nos alegra poder ayudarte. Te invitamos a que continúes visitándonos e invites a tus compañeros de clase a utilizar nuestros materiales. No dejes de comentarnos qué temas o herramientas necesitas de vez en cuando!