En muchas ocasiones la suma de fracciones nos hace pensar en las dificultades que tenemos con las matemáticas, pero con paciencia y práctica nos daremos cuenta de que esta operación es fácil de aprender. Las fracciones son números enteros que han sido divididos en varias partes y de los que tomamos un fragmento.
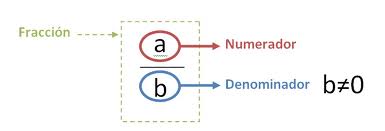
Este tipo de números están formados por dos cifras; un numerador, que es el número que se encuentra en la parte superior, y es el que representa las partes que tomamos de una unidad, y por un denominador, que se encuentra en la parte inferior, representando las partes en las que fue dividida la unidad. Hay diferentes tipos de fraccionarios; propios, impropios, decimales, etcétera. En esta ocasión utilizaremos fracciones propias para desarrollar ejemplos de sumas.
Por ejemplo: 3/4
Numerador → 3
Denominador → 4
Lo primero que debemos tener en cuenta cuando vamos a realizar una suma de fracciones es que sean homogéneas, es decir, que el denominador sea común para todas las fracciones.
Por ejemplo:
8/4 + 5/4
En este caso el denominador común es 4 y podemos continuar con la suma.
El siguiente paso es la suma directa de los numeradores:
8 + 5 = 13
Siendo el denominador común 4 tenemos que el resultado final es 13/4.
Los resultados deben ser simplificados siempre que sea posible, eso quiere decir que si la suma de fracciones que realizamos nos ha dado un resultado en el que se pueden dividir tanto el numerador como el denominador con el mismo número, hay que llegar hasta su mínima expresión.
Por ejemplo:
6/4 + 4/8 = 64/32 = 2/1
La fracción 64/32 ha sido dividida por dos hasta llegar a 2/1, y ese es el resultado final.
Pero; ¿Qué ocurre cuando el denominador es diferente?
Hay que igualarlo buscando el mínimo común denominador. Esto lo podemos hacer multiplicando los denominadores entre sí, también tenemos que multiplicar los numeradores de forma cruzada con los denominadores.
Ejemplos de suma de fracciones:
Los denominadores fueron multiplicados entre sí antes de ser simplificados, es decir; 4 por 6 = 24, y luego se dividió ese resultado entre dos, lo que nos lleva al mínimo común denominador 12. Posteriormente los denominadores simplificados individualmente se multiplican de forma cruzada con los numeradores, que luego se suman y nos da por resultado el numerador definitivo 17, este proceso que acabamos de ver nos conduce a la fracción 17 sobre 12, como vemos en la imagen anterior.
A continuación encontrarás otro ejemplo acompañado de gráficas para mayor claridad:
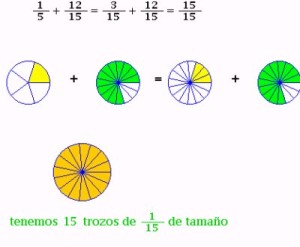
Como puedes ver en el esquema anterior se encuentra el común denominador que en esta suma es 15, se realiza la suma entre los numeradores previa simplificación, y como resultado final tenemos 15 sobre 15, lo que significa que es una unidad o número entero.
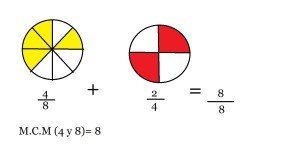
Aquí encuentras otro ejemplo que tiene diferente denominador y que también concluye en una unidad que está representada por 8 sobre 8. Pero no en todas las sumas de fraccionarios el resultado es una unidad entera, cada caso es diferente aunque tenga el mismo procedimiento para llegar al resultado.
Te anexo otro de los ejemplos de suma de fracciones :
Si tienes 1/6 + 3/12 la suma se desarrolla así;
6 * 12 = 72 = 9 → 6 * 3 = 18 → 1 * 12 = 12 → 18 + 12 = 9 + 6 = 15 → 15/9 = 5/3
Al multiplicar 6 por 12 obtenemos el denominador común 72, que podemos simplificar hasta llegar a 9. Ahora se hace la multiplicación cruzada entre denominadores y numeradores; 6 por 3 = 18 y 1 por 12 = 12, ambos resultados pueden ser divididos por dos, es decir, 18 dividido por 2 = 9 y 12 dividido por 2 = 6, esto nos da 9 + 6 = 15. Hasta ahora tenemos la fracción 15/9 que aún podemos simplificar por 3 y nos da como resultado 5/3.
Aunque algunas veces pueda parecer algo complicado las operaciones matemáticas que incluyen fraccionarios son muy sencillas de realizar y tienen un método fácil de aprender. Anímate a inventar Ejemplos de suma de fracciones para repasar lo que has aprendido hoy. Puedes tomar lápiz y papel y resolver los siguientes ejemplos:
8/10 + 3/5
2/8 + 5/6
11/24 + 5/12
Puedes seguir practicando la suma de fracciones con los ejemplos y ejercicios que encuentras con Matemáticas Modernas, así podrás desarrollar nuevas sumas que te ayudarán a profundizar en tus conocimientos.