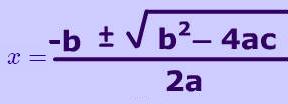 La idea es que puedas ejercitarte. Por eso pensé en proponerte algunos ejercicios de ecuaciones cuadráticas resueltas, de tal modo que puedas comprobar cómo van tus progresos.
La idea es que puedas ejercitarte. Por eso pensé en proponerte algunos ejercicios de ecuaciones cuadráticas resueltas, de tal modo que puedas comprobar cómo van tus progresos.
Antes de pasar a los ejercicios en sí mismos, te recomiendo consultar dos post que hemos compartido hace unos días y que son insumos imprescindibles si quieres dominar este tema: Clasificación de ecuaciones de segundo grado y Como resolver ecuaciones cuadráticas.
Teniendo claro el contenido de ambos post, te propongo comenzar ya mismo con los…
Ejercicios de ecuaciones cuadráticas resueltas
Te propondré en primer término las ecuaciones incrementando el nivel de dificultad en cada caso. La idea es que intentes resolverlas por tí mismo y luego compares tu trabajo con las soluciones que aportaré más abajo.
Te invito a hacer tu mayor esfuerzo y no ceder a la tentación de consultar las soluciones rápidamente.
- Ejercicios
Clasifica y resuelve las siguientes ecuaciones de segundo grado o cuadráticas:
1.- x2 −3x −4 = 0
2.- 5 x2 −6x −1 = 0
3.- 3 x2 −24 x = 0
4.- 3 ( x2 – 9) = 0
- Soluciones
1.- Se trata de una ecuación cuadrática completa. Primer paso definir quiénes son los coeficientes a,b y c. Segundo paso aplicar fórmula cuadrática para resolverla.
a= 1; b= -3 y c= 4
Resolución:
2.- Se trata de una ecuación cuadrática completa. Primer paso definir quiénes son los coeficientes a,b y c. Segundo paso aplicar fórmula cuadrática para resolverla.
a= 5, b= -6 y c= -1
Resolución:
3.- En este caso se trata de una ecuación cuadrática incompleta, en la que falta el término independiente, o sea el coeficiente c. Es posible resolver esta ecuación utilizando la fórmula cuadrática y asignando a “c” el valor cero. Pero como ya habrás leído, existe una manera más sencilla de resolverla que comienza por sacar factor común “x” de ambos términos. Como queda un producto de dos factores cuyo resultado es cero, uno de los dos tiene que ser cero y esa es precisamente la base de las dos soluciones que estamos buscando. Presta atención y compara con tus propios resultados:
4.- En este caso es una ecuación cuadrática incompleta a la que falta su término lineal (vale decir “b=0”), pero que además requiere realizar una operación previa hasta llegar a su forma tipo. He aquí los pasos para su resolución:
Te invito a estar pendiente pues en los próximos días seguiré compartiendo más propuestas de este tipo: ejercicios de ecuaciones cuadráticas resueltas para que puedas hacer tus propias prácticas y comparar resultados.
Te desafío además a realizar las verificaciones en cada caso. Siempre es más que recomendable verificar, es decir un hábito que vale la pena incorporar.
Imagen: mathwarehouse

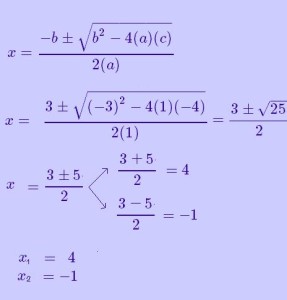
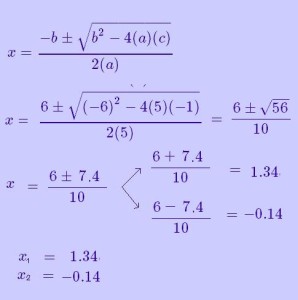





son grandiosas y les entendi