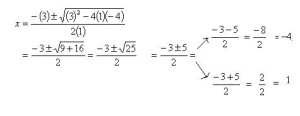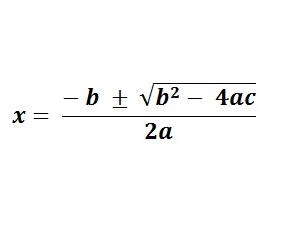 ¿Qué te parece practicar algunos ejercicios de ecuaciones de segundo grado? ¿Recuerdas cómo resolver ecuaciones cuadráticas?
¿Qué te parece practicar algunos ejercicios de ecuaciones de segundo grado? ¿Recuerdas cómo resolver ecuaciones cuadráticas?
Pues bien, el punto clave es que hay varias formas de resolver ecuaciones de segundo grad, también llamadas cuadráticas, a tal punto que éstos métodos van desde fórmulas o “recetas” (aplicables según el tipo de ecuación de que se trate) hasta la posibilidad de aplicar algunas posibilidades más intuitivas como veremos a continuación, en el primer ejemplo de nuestros…
Ejercicios de ecuaciones de segundo grado
Te propongo esta dinámica: planteo un ejercicio, analizamos la propuesta y vamos comentando cómo solucionarla. Es decir, en este caso el post de hoy está pensado para que practiques técnicas de resolución de ejercicios de ecuaciones de segundo grado, apoyándote en la guía que vamos compartiendo.
Próximamente te acercaré el clásico formato: varios ejercicios de ecuaciones de segundo grado y sus respectivas soluciones para desafiarte a resolverlas por ti mismo antes de comparar con nuestros resultados.
- Primer ejercicio:
- (x + 1) (x – 3) = 0.
He aquí una clásica ecuación cuadrática, y se supone que para resolverla podrías utilizar propiedad distributiva y multiplicar ambos factores, de tal modo de obtener una ecuación cuadrática en su forma tipo. En este caso obtendríamos una ecuación de segundo grado completa, de tal modo que identificando quiénes son los coeficientes “a”, “b” y “c”, sería factible conectarlos a la fórmula cuadrática y rápidamente obtener el valor de sus soluciones x’ y x”.
Pero, ¿por qué complicarnos si es posible pensar una alternativa? Es decir, estamos ante expresiones factoreadas, lo que nos facilita notablemente un razonamiento como el siguiente:
Si (x + 1)(x – 3) = 0, quiere decir que por lo menos uno de las dos expresiones entre paréntesis obligatoriamente vale cero.
En expresión matemática, escribiría que
x + 1 = 0 ó x – 3 = 0
Entonces para el primer caso x = – 1 y para el segundo x = 3 (Únicosvalores que anulan cada una de las expresiones).
Por tanto la pareja de soluciones buscada es la siguiente:
La solución es x’=-1 y x”= 3
Este razonamiento es aplicable aún si se te propone un ejercicio de ecuaciones de segundo grado con formato típico; si tienes posibilidad de factorear dicha propuesta puedes utilizar esta técnica para resolverlo.
He aquí un ejemplo guiado:
- Segundo ejercicio:
x 2 – 3 x – 4 = 0.
Es sencillo convertir esta ecuación a factores fácilmente:
(x + 1) (x – 4) = 0
x + 1 = 0 ó x – 4 = 0
Los valores que anulan esas expresiones son respectivamente
x = -1 // x = 4
Por tanto la pareja de soluciones buscada es la siguiente:
x’=-1 y x”= 4
- Tercer ejercicio:
En este caso proponemos una resolución utilizando la clásica fórmula cuadrática, también llamada simplemente “Báskara” en algunos países y que puedes ver en nuestra imagen de portada. Veamos la propuesta y cómo resolverla:
x2 + 3x – 4 = 0
Lo primero que debes hacer es identificar quiénes son los coeficientes “a”, “b” y “c”. En este caso son respectivamente:
a =1 / b = 3 / c =-4
De este modo, la aplicación de la fórmula y el arribo a las soluciones sería así:
Las soluciones en este caso son entonces:
x’=-1 y x”= 4
Te invito a estar pendiente de nuestro próximo post donde te propondré ejercicios de ecuaciones de segundo grado, tú deberás resolverlas y podrás comparar resultados con nuestras respuestas.
Imagen: ncalculators