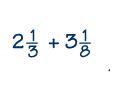Recordemos que las fracciones son números que se han dividido y se representan con dos cifras, una ubicada arriba que indica las partes que tomamos de la unidad y la otra abajo que indica las partes en las que se dividió la unidad. Luego de conocer y repasar las fracciones aprendemos que existen diferentes clases con las que también podemos realizar operaciones matemáticas. A continuación veremos una clase de fracciones que están compuestas por un número entero y un número fraccionado y se denominan mixtas.
Ejercicios de fracciones mixtas:
El número entero que compone a las fracciones mixtas puede ser de una o más unidades, y la fracción por sí sola es la que representa la parte adicional que se ha tomado de otra unidad dividida en cierta cantidad de partes, esta clase de fracciones se escriben y se grafican de esta manera:
Ahora que hemos recordado cómo se ve una fracción mixta demos inicio a los ejercicios con sumas y restas de fracciones mixtas.
La primera de las operaciones es la suma, que con esta clase de fracciones se realiza de la siguiente manera. Por ejemplo:
En este caso cada fracción debe ser convertida a fracción impropia, para esto, el número entero de cada fracción mixta debe ser multiplicado por el denominador y sumado con el numerador, y todo conserva el mismo denominador de la fracción. La suma se realiza de aquí en adelante como una suma de fracciones normal, ten en cuenta que el denominador sea igual en todas las fracciones, si son distintos hay que igualarlos de la misma forma que a una fracción convencional, con el mínimo común múltiplo.
Continuemos con el ejemplo anterior:
2 ⅓ = 2 × 3 + 1 = 7
3 ⅛ = 3 × 8 + 1 = 25
Las fracciones se convierten en impropias y se resuelve normalmente:
7/3 + 25/8 = 131 /24
La resta de fracciones mixtas se realiza de la misma forma que con las fracciones normales, de igual manera si el denominador es distinto debemos encontrar el mínimo común múltiplo.
Resolvamos los siguientes ejercicios:
2⅔ + 3⅛ =
2 × 3 +2 = 8
3 × 8 +1 = 25
= 8/3 + 25/8 = 89/24
3¾ – 2⅓ =
3 × 4 + 3 = 15
2 × 3 + 1 = 7
= 15/4 – 7/3 = 17/12
A continuación encuentra otros ejercicios para resolver:
Encuentra la respuesta correcta.
Recuerda que la práctica constante de estos y otros ejercicios te permitirá mantener frescos tus conocimientos y profundizar cada vez más en los temas de tu interés.
Puedes encontrar en Matemáticas Modernas más ejemplos y ejercicios de fracciones de diferentes clases, diviértete practicando.