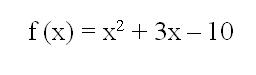 Resolver ejercicios de funciones no sólo no es difícil sino que puede hasta llegar a ser muy divertido. ¿Sabes cuál es la clave? Que seas capaz de comprender claramente el concepto de función matemática y que en base a ello, puedas aprender a reconocer los distintos tipos de ejercicios de funciones que se te pueden llegar a presentar así como las estrategias para resolverlos.
Resolver ejercicios de funciones no sólo no es difícil sino que puede hasta llegar a ser muy divertido. ¿Sabes cuál es la clave? Que seas capaz de comprender claramente el concepto de función matemática y que en base a ello, puedas aprender a reconocer los distintos tipos de ejercicios de funciones que se te pueden llegar a presentar así como las estrategias para resolverlos.
Vamos al análisis que te proponía antes, es decir reconocer los diferentes tipos de
Ejercicios de funciones
Comencemos por los más clásicos, vale decir aquellos que te desafían a construir la representación gráfica de una función. Está claro que no siempre podrás hacerlo y que todo depende del tipo de función que se te proponga y del nivel académico en que te encuentres. No obstante parto de la base del sentido común: si tu maestro o profesor te propone un ejercicio de este tipo es porque la función en cuestión en sencilla de representar en forma gráfica. Tal podría ser el caso de una función lineal, como f (x) = 2x + 3 , o de una función cuadrática clásica, como por ejemplo la siguiente, también comúnmente conocida como función polinómica de segundo grado.
¿Cómo se resuelven este tipo de ejercicios? Es sencillo y te recomiendo tener a mano una hoja de papel cuadriculado y por lo menos una regla para poder construir el gráfico con mayor exactitud y precisión. El primer paso es construir una pequeña tabla de valores, donde a la izquierda colocas los valores que irás adjudicando a la “x” (por eso se le llama variable independiente, es decir tú le das el valor que quieres) y realizarás las operaciones que te indica la expresión de la función, de modo de calcular el valor en función de “x” en cada caso, lo que en definitiva será la coordenada del eje “y” de tu sistema cartesiano de ejes. De este modo, cada “x” tendrá su “y”, por lo que si construyes tu par de ejes cartesianos podrás ir marcando los puntos del gráfico que debería ser una recta (en el caso de las funciones lineales o de primer grado) o una parábola (en el caso de las funciones cuadráticas de segundo grado).
Otras veces no se te pide que realices la representación gráfica exacta de una función, sino que realices el estudio de una función. Un estudio de este tipo no es ni más ni menos que un análisis que te permite determinar cómo será el gráfico de esa función en particular e incluso te permitirá dibujar un croquis o esquema de la misma.
Por ejemplo en el caso del estudio de una función de segundo grado, una vez que el profesor te de la expresión algebraica de la misma, tú podrás determinar con bastante exactitud como se comportará ésta en el plano, determinando los siguientes parámetros:
1) Concavidad (está determinada por el signo del coeficiente del término de segundo grado; en nuestro ejemplo anterior sería positiva)
2) Ordenada al origen (está determinada por el valor que surja al anular todos los términos en X; coincide con el término independiente de la expresión clásica de la función, en nuestro ejemplo anterior sería -10). Marca el punto de corte con el eje de las ordenadas o eje vertical.
3) Raíces o soluciones (las hallarás convirtiendo la función en una ecuación y esas soluciones -que podrían ser iguales e incluso no existir, te revelan el o los puntos de corte del gráfico de la función con el eje horizontal o de las abscisas)
4) Vértice (será un máximo o un mínimo, dependiendo de la concavidad de la función).
Imágenes: solving-math-problems