Las gráficas funciones trigonométricas tienen propiedades como: dominio, alcance, máximo, mínimo, periodo y algunas otras. De cada función te mostraré sus características y su gráfica:
Funciones trigonométricas gráficas
Función |
Gráfica |
| Seno | 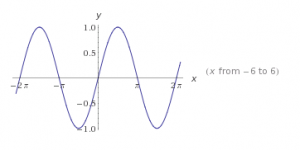 |
| Coseno | 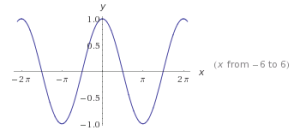 |
| Tangente | 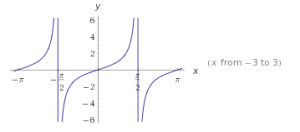 |
| Cotangente | 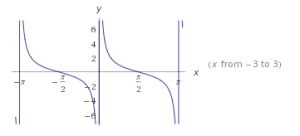 |
| Secante | 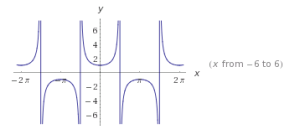 |
| Cosecante | 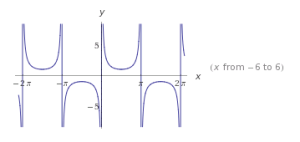 |
CARACTERÍSTICAS
SENO
El ciclo de la función seno comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en (0,0)
El eje de referencia es: eje “x”.
El punto máximo es: (π/2,1)
El punto mínimo es: (3π/2,-1)
Su período: 2π.
COSENO
El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales.
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en: (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (0,1) y (2π,1)
El punto mínimo es: (π,-1)
Su período: 2π
TANGENTE
El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a (π/2)±nπ
Alcance: el conjunto de todos los números reales.
Cruza el eje de “y” en (0,0)
El eje de referencia es: el eje “x”
El punto máximo es:
El punto mínimo es:
Su período: π
Asíntotas: x=±π/2
CONTANGENTE
El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a ±nπ
Alcance: el conjunto de todos los números reales.
No cruza el eje de “y”
El eje de referencia es: el eje “x”.
Su período: π
asíntotas: x=±nπ
SECANTE
El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.
Tiene tres asíntotas verticales.
Dominio: el conjunto de números reales excepto los múltiplos impares de π/2
Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2
COSECANTE
El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.
Tiene tres asíntotas.
Dominio: el conjunto de números reales excepto los multiplos impares de π/2
Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2