Para obtener la ecuación de la hipérbola con centro en un punto cualquiera hay que definir que es una hipérbola, esta es el lugar geométrico de los puntos de un plano cuya diferencia de distancias a dos puntos fijos F y F’ es una cantidad constante que se representa por 2a. Así para cualquier punto P de la curva, se tiene PF – PF’ = 2a.
Elementos de la hipérbola
- La curva es abierta y consta de dos ramas.
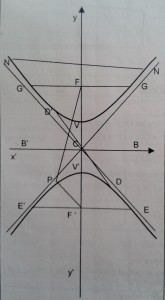
- Los puntos fijos F y F’ se llaman focos y la longitud FF’ distancia focal que se designa por 2c.
- El punto medio de FF’ es el centro de la hipérbola (c).
- Los segmentos PF y PF’ que unen un punto cualquiera de la hipérbola con los focos se llaman radios.
- Un segmento que une dos puntos NN’ cualesquiera de la hipérbola se denomina cuerda.
- Una cuerda que pasa por el centro, como DD’ se llama diámetro.
- El diámetro que pasa por los focos se llama eje real, focal o transverso VV’ que se designa por 2a. Sobre la recta perpendicular al eje focal, que pasa por el centro O y que no corta a la curva, se considera un segmento BB’, llamado eje conjugado o imaginario que se designa por 2b.
- Las intersecciones V, V’ del eje focal con la curva son los vértices de la hipérbola.
- Las cuerdas EE’ y GG’ que pasan por los focos y son perpendiculares al eje mayor son los lados rectos de la hipérbola.
- Excentricidad de una elipse es la razón de la semidistancia focal al semieje mayor (c/a) y se representa por e. Para
- que sea hipérbola c>a.
- La curva está comprendida dentro del ángulo formado por las diagonales del rectángulo, cuyas dimensiones son 2a y 2b. Estas rectas se llaman asíntotas.
Propiedades de la hipérbola
- El eje real es igual a la cantidad constante VV’ =2a
- El eje conjugado es igual a BB’ = 2b
- La distancia focal FF’ =2x
- Los ejes se cortan en su punto medio c.
- Relación entre los semiejes y la semidistancia focal el: \begin{align}c^{2} =a^{2} +b^{2}\end{align}
- La excentricidad siempre es mayor que 1.
Formulario para la hipérbola con centro en un punto cualquiera
|
Formula de: |
Eje transverso “x” |
Eje transverso “y” |
|
Ecuación de la hipérbola |
\begin{align}\frac{(x-h)^{2}}{a^{2}} – \frac{(y-k)^{2}}{b^{2}} =1\end{align} |
\begin{align}\frac{(y-k)^{2}}{a^{2}} – \frac{(x-h)^{2}}{b^{2}} =1\end{align} |
|
Focos |
F(h + c, k) F’(h – c, k) |
F(h, k + c) F’(h, k – c) |
|
Vértices |
V(h + a, k) V’(h – a, k) |
V(h, k + a) V’(h, k – a) |
|
Extremos del eje conjugado |
B(h, k + b) B’(h, k – b) |
B(h + b, k) B’(h – b, k) |
|
Longitud del eje real o transverso |
VV’=2a |
VV’=2a |
|
Longitud del eje imaginario o conjugado |
BB’=2b |
BB’=2b |
|
Distancia focal |
FF’=2c |
FF’=2c |
|
Excentricidad |
e=c/a |
e=c/a |
|
Longitud del lado recto |
\begin{align} {LR} = \frac{2b^{2}}{a}\end{align} |
\begin{align} {LR} = \frac{2b^{2}}{a}\end{align} |
|
Relación pitagórica |
\begin{align}c^{2} =a^{2} +b^{2}\end{align} |
\begin{align}c^{2} =a^{2} +b^{2}\end{align} |
|
Ecuaciones de las asíntotas |
y – k = ± b/a (x – h) |
y – k = ± b/a (x – h)
|