 La Homotecia en el plano es una de las cuatro transformaciones en el plano a las que ya hicimos mención en un post anterior. En algunos cursos se le llama ampliación o reducción de figuras en el plano, pero el concepto es el mismo y te invito a ver con detalle de qué se trata.
La Homotecia en el plano es una de las cuatro transformaciones en el plano a las que ya hicimos mención en un post anterior. En algunos cursos se le llama ampliación o reducción de figuras en el plano, pero el concepto es el mismo y te invito a ver con detalle de qué se trata.
Homotecia en el plano
Recordemos que habíamos clasificado a las transformaciones en el plano en dos tipos:
- Transformaciones isométricas en el plano, son aquellas que mantienen la forma y el tamaño de la figura en cuestión, vale decir no se altera la longitud de sus lados (si hablamos de un polígono) ni otras medidas claves (como el radio si hablamos de una circunferencia).
- Transformaciones no isométricas en el plano, son aquellas que -por el contrario- alteran una o más de las dimensiones de las figuras. Por ejemplo, un caso muy frecuente es que a consecuencia de una transformación, se varíe proporcionalmente el tamaño de los lados y en consecuencia la superficie.
Precisamente a éste último concepto responde una homotecia en el plano. Por tanto vamos a enunciar una definición para que te queden bien claras las cosas:
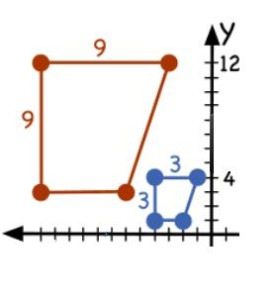
La homotecia es una transformación en el plano, que nos permite obtener figuras a escala, manteniendo sus proporciones. ¿Qué quiere decir esto? que si hablamos por ejemplo de polígonos, se mantendrán iguales sus ángulos pero aumentará o disminuirá la longitud de sus lados.
Éste último detalle es importante porque será una homotecia directa si la figura se agranda o una homotecia inversa si la figura disminuye de tamaño. Para sintetizar el concepto decimos que una figura y su homotética tendrán
- igual forma
- diferente tamaño
¿Cómo obtener figuras homotéticas?
El procedimiento es muy sencillo, de hecho podemos elegir dos formas
- con ejes cartesianos
- con centro de homotecia
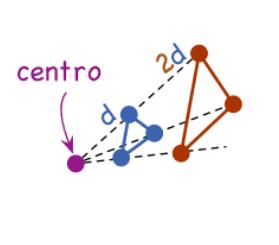
El más común de los procedimientos es utilizar un centro de homotecia. Como útiles de geometría, necesitarás una regla y un compás (este último no es imprescindible si la regla que utilizas, está marcada con centímetros y milímetros).
El profesor te dará la figura, la razón de la homotecia y el centro de homotecia. Tú sigue los siguientes pasos:
- Une con una recta, cada vértice de la figura con el centro de homotecia. Presta atención que te digo una recta, es decir que esta unión debe pasar por cada pareja de puntos, pero no termina en ellos.
- Queda definido entonces, en cada recta, un segmento entre el vértice en cuestión y el centro de homotecia. Aumenta (si te piden homotecia directa) o disminuye (si se trata de una homotecia indirecta) la longitud de esa línea tomando en cuenta la razón de la homotecia (también llamado factor escalar).
- Une los nuevos puntos obtenidos sobre cada una de las rectas: ni más ni menos, se trata de los vértices de la nueva figura.
Otros nombres para la homotecia
Sabemos que tenemos lectores de muchos países, por lo que es importante señalar que a la homotecia se le conoce o enseña con otros nombres:
algunos maestros o profesores llaman a la homotecia dilatación, contracción, compresión, alargamiento o reescalamiento. No te preocupes, todo significa lo mismo.
Imagen: virtualnerd