¿Que son los números primos?, quizás te hayas preguntado porque son únicos estos números y que los hace tan especiales. ¿Que aplicaciones tienen los números primos en las matemáticas y en la vida real?
Cuando estudiamos matemáticas nos damos cuenta que los números se clasifican en distintas categorías ya sea números reales, números enteros, números irracionales pero y que de los números primos.
Los números primos son simplemente cualquier numero que solo se pueda dividir entre 1 y el mismo, así tenemos que 2 es primo porque solo el 2 y el 1 lo pueden dividir de manera exacta.
Dije simplemente porque eso los hace diferentes a los demás números, el hecho de que los números primos solo puedan ser divididos entre 1 y ellos mismos tiene varias implicaciones.
Así los números 2, 3, 5, 7, 11, 13,17 serian números primos porque solo el 1 y el mismo número los dividen de manera exacta, el 4, 6, 8, 12 no son primos ya que el numero 2 los divide de manera exacta.
La definición de un número primo es:
“Un numero entero mas grande que uno, si sus divisores positivos solo son el numero uno y el mismo”
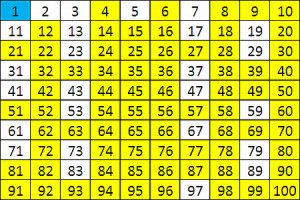
Con esta definición podemos construir una lista de los números primos menores a 100 como esta en la que los números primos están de color amarillo:
Hay un teorema en matemáticas (recordemos que un teorema es una suposición que puede ser demostrada) llamada teorema fundamental de aritmética que dice que:
“Todo numero entero mayor que 1 puede expresarse únicamente como la multiplicación de números primos.”
Por ejemplo:
| 40 | 2*2*2*5 |
| 100 | 2*2*5*5 |
| 88 | 2*2*2*11 |
Un ejemplo más explicito factorizando el número 2100:
|
2100
|
2
|
|||
|
1050
|
2
|
|||
|
525
|
3
|
2100= 2*2*3*5*5*7
|
||
|
175
|
5
|
|||
|
35
|
5
|
|||
|
7
|
7
|
|||
De hecho este teorema es una de las razones por la que a 1 no se le considera como numero primo veamos porque no, el teorema dice:
“Todo numero entero positivo mayor que 1 puede expresarse únicamente como la multiplicación de números primos.”
Dicho de otra manera como “Cualquier numero entero mayor a uno puede expresarse como el producto de un cierto grupo de números primos, con los números primos como factores escritos en orden descendiente”
Supongamos que el numero uno si es un numero primo entonces expresemos el numero 30 como 2*5*3 pero también podría expresarse como 2*5*3*1 ya que la multiplicación por el numero uno es neutra ya que no cambia su valor.
Dado que el numero 30 se podría expresar 2*5*3 pero también podría expresarse como 2*5*3*1 y estamos considerando al numero uno como primo, entonces nuestro teorema se contradice ya que dice que únicamente se puede expresar como la multiplicación de un cierto grupo de números primos.
De hecho el numero 1 es inútil ya que no nos provee de información al factorizar o expresar un numero x = x*1 = x*1*1 = x*1*1*1…
Descubrimiento de los números primos
 Los antiguos griegos conocían ya estos números e incluso Euclides (300 A.C) un matemático griego probo que el numero de primos es infinito, esto quiere decir que dada una lista de números primos finita siempre habrá un numero primo que no este en esa lista.
Los antiguos griegos conocían ya estos números e incluso Euclides (300 A.C) un matemático griego probo que el numero de primos es infinito, esto quiere decir que dada una lista de números primos finita siempre habrá un numero primo que no este en esa lista.
El libro elementos de Euclides contiene importantes teoremas sobre los números primos como la infinitud de los números primos, y el teorema fundamental de la aritmética
La criba de Eratóstenes atribuido a Eratóstenes de Cirene (276-194 A.C.) un matemático y geógrafo griego quien descubrió la medida de la circunferencia de la tierra solo observando la sombra que proyectaba un palo, ideo este método
La criba consiste en ir marcando sucesivamente los múltiplos de 2, de 3, de 4, etc. de una lista de números naturales, los que van quedando sin marcar son los números primos:
Aplicaciones de los números primos
Durante mucho tiempo en la historia de la matemática se asumió que los números primos solo tenían utilidad en las matemáticas puras, un ejemplo seria facilitando las operaciones con radicales o raíces.
Para este ejemplo usaremos radicales, si aun no los conoces no importa puedes usar tu calculadora.
Un ejemplo ¿Si no tuvieras una calculadora como resolverías esta raíz cuadrada?
√324
Resolviendo raíz de 324 usando los números primos.
Descomponemos 324 en sus factores primos dividiendo:
|
324
|
2
|
|||
|
162
|
2
|
|||
|
81
|
3
|
324 = 2*2*3*3*3*3
|
||
|
27
|
3
|
|||
|
9
|
3
|
|||
|
3
|
3
|
|||
|
1
|
||||
Simplificamos la raíz
√(2*2*3*3*3*3)
Simplificamos usando leyes de radicación por lo que sacamos raíz a cada factor de 324 y lo ponemos fuera del radical.
√(4*9*9)
2*3*3
18
La raíz cuadrada seria 18
 En la vida real un uso es la criptografía que es codificar mensajes o cifrarlos por ejemplo el cifrado en páginas de internet donde se necesita seguridad al realizar transacciones monetarias como la pagina web de un banco o en el comercio electrónico, usando varios algoritmos de cifrado como el RSA.
En la vida real un uso es la criptografía que es codificar mensajes o cifrarlos por ejemplo el cifrado en páginas de internet donde se necesita seguridad al realizar transacciones monetarias como la pagina web de un banco o en el comercio electrónico, usando varios algoritmos de cifrado como el RSA.
Un ejemplo muy básico de cómo se cifra un mensaje seria este:
A cada letra del abecedario le haremos corresponder un número dos cifras.
A=01 B=02 C=03 D=04 E=05 F=06 G=07 H=08 I=09 J=10 K=11 L=12 M=13 N=14 Ñ=15 O=16 P=17 Q=18 R=19 S=20 T=21 U=22 V=23 W=24 X=25 Y=26 X=27 Y=28 Z=29
El que envía el mensaje usa este método de cifrado:
Si el número que corresponde a la letra es primo, se deja como está, y si es compuesto, se le suma un número, 5 en este caso.
A=06 B=02 C=03 D=09 E=05 F=11 G=07 H=13 I=14 J=15 K=11 L=17 M=13 N=19 Ñ=20 O=21 P=17 Q=23 R=19 S=25 T=26 U=27 V=23 W=29 X=30 Y=31 X=32 Y=33 Z=29
La palabra “Alfredo” sería 06171119050921
Para descifrar un mensaje, agrupamos el número en partes de dos cifras:
Descifrar 13211706 0613140721
Agrupamos en partes de dos cifras:
13 21 17 06 06 13 14 07 21
Y buscamos la letra correspondiente en la tabla por lo que:
13 21 17 06 06 13 14 07 21 es “Hola Amigo”
Si quieres saber mas sobre como funciona el sistema de cifrado RSA y sus implicaciones da clic aquí