Los números reales

Artículo previo Siguiente artículo

Utilizar números reales se volverá algo cotidiano a medida que avanzas en la escuela. Estamos hablando de un conjunto numérico integrado a su vez por algunos conjuntos numéricos a los que ya hemos hecho referencia (tales como los números naturales) y por otros que iremos estudiando poco a poco.

Pero me parece indispensable proponerte hoy esa visión más grande que constituyen los números Reales. Se le llama habitualmente Conjunto y se simboliza precisamente así, mediante una “R” especial que se reconoce rápidamente. Pero vamos por partes: te invito a hacer un paso a paso que recrea cómo se ha ido construyendo la identidad y composición del conjunto de…

Históricamente, el conjunto de los números reales se fue construyendo o desarrollando mediante la ampliación de la noción de “número” más básica, es decir aquellos utilizados como un instrumento con el que puedes contar y ordenar. Como recordarás le llamábamos “números naturales” y se definen como el Conjunto N. Estos son el cero, el uno y así sucesivamente dado que estamos hablando de un conjunto infinito.

Para resolver el problema de la resta entre números Naturales (¿cómo expresar el resultado de una resta cuyo primer término es menor que el segundo?) se crea el conjunto de los números enteros, habitualmente llamado conjunto Z y que se representa en una recta que los contiene a la izquierda del cero, permitiendo lugar o coexistencia con los naturales que constan al a derecha del cero. Esto puede verse claramente en la siguiente imagen:

Queda claro que el conjunto Z o de números enteros, contiene a los naturales. Dicho de otra forma cuando se adicionan los números negativos a los naturales que ya conocíamos, la totalidad de este conjunto se llaman números enteros y se representan como Z.

A continuación, para resolver el problema de las divisiones en el conjunto Z cuyo resultado no se puede expresar con los conjuntos anteriormente señalados (¿cómo expresar el resultado de una división cuyo dividendo es menor que el divisor?), es que se crea el conjunto de los números racionales identificado con la letra Q. Ni más ni menos se trata de las viejas y queridas fracciones, que expresan en los hechos una división y que además pueden escribirse en la mayoría de los casos como un número decimal, por ejemplo la fracción 3/2 que también puede expresarse como el decimal 1,5 con total exactitud.

Y me remito a esta última expresión: “con total exactitud” para dar lugar al siguiente conjunto numérico, esto es los números irracionales. ¿Por qué? Porque no siempre estamos hablando de fracciones (u otras operaciones) que pueden ser expresadas como decimales exactos. Ya desarrollamos este tema en otro post dedicado a los números irracionales, que te invito a releer.

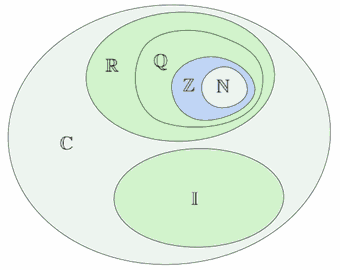
Ahora bien ¿Cómo es que toda este camino nos conduce a los números reales, tema de hoy? Muy sencillo: el conjunto que contiene a los números racionales y a los irracionales se llama números reales.

Para clarificar aún más el concepto, podemos expresar esta idea visualizando la siguiente imagen, sobre la que vale aclarar que no es del todo exacta, porque como recordarás, no podríamos “encerrar” a todos los números anteriores enun diagrama de Venn, porque se trata de conjuntos numéricos infinitos. En ese sentido, la representación mediante una recta numérica sigue siendo más acertada.