¿Qué es el Lugar geométrico de Thales? Te propongo aprender acerca de este tema y realizar algunos ejercicios interactivos a partir de esta primera lección.
Como primer paso, te propongo definir qué es un lugar geométrico. Se llama lugar geométrico, a un conjunto de puntos que cumplen con una condición o propiedad específica. Este conjunto de puntos, puede estar en el espacio o en el plano.
Uno de los lugares geométricos más conocidos en el plano, es lo que conocemos habitualmente como circunferencia. Como sabes, una circunferencia se constituye por el conjunto de puntos de un plano, que equidistan de otro punto del mismo plano llamado centro.
Del mismo modo, si llevamos la misma definición al espacio, queda definida una esfera, que no es ni más ni menos que el lugar geométrico de los puntos del espacio, que equidistan de otro punto del mismo, llamado centro.
Una vez definido en forma genérica este concepto vamos a aprender específicamente acerca del…
Lugar geométrico de Thales
Como su nombre lo indica, este Lugar geométrico se atribuyó al matemático y filósofo griego Thales de Mileto, quien nació en el 625AC y murió en el 547AC.
Éste es el enunciado:
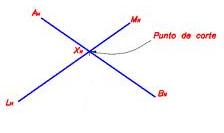
“Todo punto C del plano, que es vértice de un ángulo recto cuyos lados pasan por los extremos de un segmento AB, pertenece a una circunferencia de diámetro AB (excluyendo A y B). De aquí se deduce que el triángulo ABC, tiene un ángulo recto con vértice en C.”
Precisamente, esa circunferencia es lo que se llama el Lugar geométrico de Thales.
Este enunciado, da lugar a lo que se conoce como Teorema recíproco del Lugar geométrico de Thales, cuyo enunciado es el siguiente:
“Todo punto C del plano, que forma parte de una circunferencia de diámetro AB (excluyendo de la misma a A y a B), es vértice de un ángulo recto, cuyos lados pasan por los extremos A y B, del mencionado segmento AB.
Demostración
El reto es demostrar o probar matemáticamente, que efectivamente el ángulo de vértice C, mide 90º.
Utilizaremos para la demostración a la siguiente figura de análisis que te invito a observar cuidadosamente a medida que vas siguiendo la demostración.
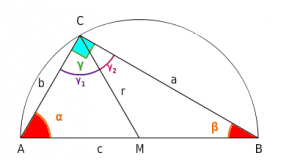
Observa en primer término que quedan definidos dos triángulos: AMC y CMB. Ambos son isósceles, pues ambos tienen un par de lados iguales que corresponden a los radios de la circunferencia de centro M.
Teniendo en cuenta eso, decimos que los ángulos adyacentes a su base también son iguales, por lo que se cumple que el ángulo:
γ = γ 1 + γ 2
y como α = γ 1 y β = γ 2, podemos decir que:
γ = α + β
Como la suma de los ángulos interiores de un triángulo es 180º, podemos decir que la suma de α + β + γ = 180º , de donde despejaríamos la ecuación
180º = 2 ( α + β )
De donde dividiendo entre 2, tenemos que
90º = α + β = γ
que es precisamente lo que queríamos probar, vale decir que γ, el ángulo total que conforma el vértice C, es igual a 90º, o sea c es recto.
Imagen: philosofait
