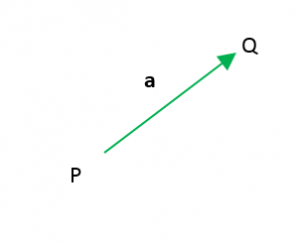
La magnitud de un vector es la distancia entre el punto inicial P y el punto final Q de un vector. La magnitud de un vector se representa de la siguiente manera:
\begin{align}\left| \overset{\rightarrow}{{PQ}} \right|\end{align}
y el vector que empieza en P y termina en Q se escribe como:
\begin{align}\overset{\rightarrow}{{PQ}}\end{align}
Un vector es una cantidad que tiene magnitud, dirección y sentido, por ejemplo la fuerza, el desplazamiento o la velocidad.
Magnitud de un vector
La magnitud de un vector se puede calcular dependiendo de los datos que se tengan:
- Si se conocen las coordenadas de los dos puntos del vector:
Se pueden obtener magnitud de vectores con sólo sustituir en la fórmula de distancia:
\begin{align} \sqrt{( x_{2} -x_{1} )^{2} + ( y_{2} -y_{1} )^{2}} \end{align}
- Si se conocen las componentes del vector
Un vector también se puede expresar como <-2, 3>, cada número se llama componente, en este vector el -2 representa la componente en “x” y el 3 representa la componente en “y”.
Para obtener la magnitud del vector <x, y> se utiliza la siguiente fórmula:
\begin{align} \sqrt{ x^{2} + y^{2} } \end{align}
Dirección de un vector
La dirección de un vector es la medida del ángulo que hace con el eje “x” (línea horizontal).
Una de las fórmulas siguientes puede ser usada para encontrar la dirección de un vector:
\begin{align}\tan \theta = \frac{y}{x}\end{align}
ó
\begin{align}\tan \theta = \frac{y_{2} -y_{1}}{x_{2} -x_{1}}\end{align}
( x1 , y1 ) es el punto inicial “P” y ( x2 , y2 ) es el punto terminal “Q”.