 Luego de aprender qué son las ecuaciones simultáneas de primer grado, te propongo comenzar a aprender el método de igualación para ecuaciones simultáneas.
Luego de aprender qué son las ecuaciones simultáneas de primer grado, te propongo comenzar a aprender el método de igualación para ecuaciones simultáneas.
Te recuerdo que a las ecuaciones simultáneas también se las llama sistemas de ecuaciones de primer grado. En este caso y para aprender paso a paso cada uno de los métodos, vamos a comenzar por un sistema de ecuaciones simultáneas de primer grado con dos incógnitas.
Como señalé hace pocos días, aprenderemos todos los métodos trabajando sobre un mismo sistema de ecuaciones simultáneas. Te recomiendo ir coleccionando o siguiendo con suma atención cada uno de los post donde enseñaré los métodos, de modo que puedas elegir aquel o aquellos que sean más sencillos para ti.
Toma nota y no tardarás en…
Resolver ecuaciones simultáneas, método de igualación
El sistema de ecuaciones simultáneas elegido es:
Es el primero de los métodos algebraicos que estudiaremos y que se usan para resolver sistemas de ecuaciones simultáneas. En este caso, hablamos de dos ecuaciones lineales con dos incógnitas.
¿Por qué se llama método de igualación?. Este método consiste en despejar la misma incógnita de las dos ecuaciones y posteriormente igualar (de ahí su nombre) los segundos miembros de esos despejes, vale decir las dos expresiones algebraicas resultantes.
De este modo queda una ecuación de primer grado con una sola incógnita que debes resolver, hallando la incógnita. Sustituyendo ese valor en las dos ecuaciones originales y despejando la otra incógnita, resolverás el sistema inicial.
Te propongo un paso a paso bien claro y conciso.
1) Despejamos la misma incógnita de las dos ecuaciones. En este caso elegimos despejar la incógnita x, de ambas ecuaciones obteniendo los despejes siguientes:
2) Igualamos los dos segundos miembros de ambas igualdades
3) Resolvemos esta ecuación hasta hallar el valor de “y”
-17 y = -32 + 15
– 17 y = -17
y= -17 / – 17
y = 1
4) Sustuimos el valor de “y” hallado en las dos ecuaciones simultáneas originales.
a) 3 x + 2 (1) = 8
b) 4 x – 3 (1) = 5
5) Resolvemos las ecuaciones, el valor de “x” que nos dé en ambos casos debería ser el mismo. Veamos los casos uno por uno:
a) 3x + 2 = 8
3x = 8 – 2
3x = 6
x = 6/3
x = 2
b) 4x – 3 = 5
4x = 5 + 3
x = 8 / 4
x = 2
6) Con ambos resultados se procede a la verificación de las dos ecuaciones simultánea. Si todo está correcto, deben verificarse las dos igualdades. Vamos paso a paso como en el ítem anterior
a) 3 x + 2 (1) = 8
3 (2) + 2 (1) = 8
6 + 2 = 8
8 = 8
b) 4 x – 3 (1) = 5
4 (2) – 3 (1) = 5
8 – 3 = 5
5 = 5
Como puedes comprobar, el método es sencillo ya que puedes resolver las ecuaciones simultáneas en unos pocos pasos y dado que cuentas con la posibilidad de verificar los resultados, podrás comprobar con total certeza si los valores que has hallado en cada caso para cada incógnita son los correctos.
Existen varios métodos algebraicos más; de ellos veremos el método de sustitución, el método de reducción y el método de matrices o determinantes. A ellos sumaremos posteriormente el método gráfico.
Te describo esto último a manera de plan, para invitarte a estar pendiente de todos esos post que compartiremos en los próximos días. No dejes de practicar este método, en pocos días te propondré una serie de ejercicios para que puedas hacerlo sin molestarte en buscar propuestas de los mismos.
Imagen: aretio

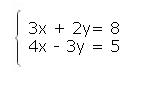
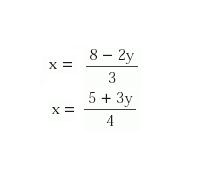
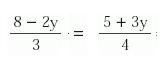
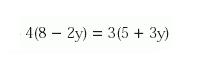


No hay respuetas