El tema de los números complejos puede confundir a los estudiantes de matemáticas, y va entrelazado con los números imaginarios, pues la expresión de los números complejos se componen de números reales e imaginarios. A continuación encontrarás la explicación de este tema con algunos ejemplos que te ayudarán a distinguir todas sus partes.
Números complejos:
Los números complejos son aquellos que están compuestos por una parte real y un componente imaginario, estos son números que se escriben de la forma a + bi, siendo el número real a y el componente imaginario bi, es decir:
2 + 3i =
2 Es el número real
3i Es el componente imaginario
La parte imaginaria está compuesta por un número real y una unidad imaginaria que está simbolizada por “i”.
Cuando b = 0, significa que el número complejo sólo tiene parte real, pero cuando tenemos a = 0, entonces decimos que el número complejo sólo tiene parte imaginaria, o sea, que los números reales e imaginarios puros están contenidos en el conjunto de los números complejos, y este conjunto se representa por una C mayúscula.
Por ejemplo tenemos que:
-6, 2/3, √2, son números reales y también números complejos.
2i, -√3i, -3/5i, son números imaginarios puros y también números complejos.
Los números complejos pueden estar representados de diferentes formas; cuando se encuentra escrito de la forma a + bi se dice que se encuentra de la forma binómica, cuando aparece escrito como par, (a + b) se le llama una pareja ordenada.
La representación gráfica de los números complejos se puede realizar de esta forma:
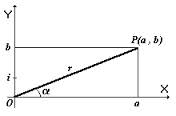
Si sobre el eje de abscisas se representa la parte real a del número complejo a + bi, y sobre el eje de ordenadas la parte imaginaria b, el número complejo a + bi puede representarse por el punto P del plano de coordenadas (a, b).
Tenemos entonces que a cada número complejo a + bi le corresponde un punto P que se llama su afijo, y a cada punto le corresponde un número complejo recíprocamente, de esta forma queda establecida una aplicación biyectiva entre los puntos del plano y los números complejos. El origen de coordenadas O y el punto P determinan un vector OP, que podemos considerar la representación vectorial del número complejo a + bi. Se le llama módulo a la longitud r del vector OP del número complejo a + bi, entonces tenemos que r = √a²+b².
La aplicación biyectiva entre números complejos y puntos del plano permite afirmar que se puede considerar a un número complejo como un par ordenado de números reales.
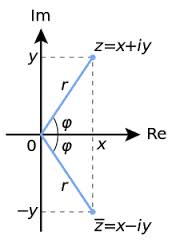
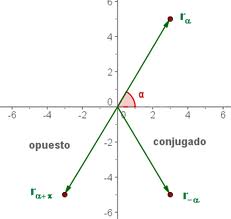
Los números complejos también pueden ser complejos conjugados y complejos opuestos:
Se llaman conjugados a dos complejos que tienen iguales sus componentes reales y sus componentes imaginarias cambiadas de signo. Por ejemplo: 5 + 3i y 5 – 3i; a + bi y a – bi.
Se les llama opuestos si sus dos componentes son opuestos, es decir, 5 + 3i y -5 – 3i; a + b y –a – b.