 ¿Qué son los números imaginarios? ¿Alguna vez te encontraste con ellos al resolver ejercicios? Probablemente sí… y te invito a conocer mejor acerca de este tema, de modo de comprender más de qué estamos hablando y en qué casos se define una solución o soluciones (por ejemplo de ecuaciones de primer y segundo grado), como un número imaginario.
¿Qué son los números imaginarios? ¿Alguna vez te encontraste con ellos al resolver ejercicios? Probablemente sí… y te invito a conocer mejor acerca de este tema, de modo de comprender más de qué estamos hablando y en qué casos se define una solución o soluciones (por ejemplo de ecuaciones de primer y segundo grado), como un número imaginario.
Veamos cómo podríamos responder a cualquiera de las siguientes preguntas; por ejemplo ¿cuál es la raíz cuadrada de un número negativo? ¿Sabías que ningún número real multiplicado por sí mismo nunca producirá un número negativo?
Si te propones encontrar la raíz cuadrada de 4 es bastante simple: 2 o -2 multiplicado por sí mismo da como resultado, 4. Sin embargo…, no hay ninguna respuesta sencilla para el caso de que te propongas hallar la raíz cuadrada de -4.
Otra situación posible y que puede suceder cuando estés resolviendo una ecuación cuadrática o de segundo grado, sería la siguiente: ¿qué haces cuando un discriminante es negativo y deberías tomar su raíz cuadrada?
Es precisamente para dar respuesta a este tipo de casos, que entran en juego los…
Números imaginarios
En pocas palabras, los matemáticos han convenido en dar respuesta a estos casos diciendo por ejemplo, que la raíz cuadrada de -1 debe ser representada por la letra i.
Algunos datos básicos que debes saber acerca del famoso “número i”, son los siguientes:
1) i , no es una variable.
2) i no puede ser encontrado en la recta numérica que contiene los números reales.
3) i no es un número real.
Otra definición interesante
Algunos profesores, entre los que me incluyo, cuando llega el momento de introducir a los alumnos en este tema, elegimos hacerlo precisamente del modo opuesto: no ejemplificando o partiendo de ejemplos vinculados a una raíz cuadrada, sino pensando .. ¿qué pasa cuando elevamos un número imaginario al cuadrado? Esa es la clave para esbozar una definición diferente. Veamos cuál es…
Un número es imaginario, si cuando se eleva al cuadrado (vale decir, se multiplica por sí mismo) nos da un resultado negativo.
Vamos a probar con algunos números elegidos al azar, a ver si podrían entrar en el perfil de esta definición…
3 * 3 = 9 (nos da un número positivo)
-3 * -3 = 9 (también nos da un número positivo)
0,2 * 0,2 = 0,04 (se trata nuevamente de un número positivo)
0 * 0 = 0 (no es positivo, pero tampoco negativo. Es cero)
¿Sabes por qué pasa esto? Porque en todos los casos hemos trabajado (es decir elevado al cuadrado) a los números reales.
Vamos a “forzar” la situación y escribamos un número imaginario llamado i, asegurando lo siguiente:
Si te pones a pensar, el hecho de admitir que exista un número que cumpla dicha condición, podría ser muy útil para resolver o -mejor dicho dar respuesta- algunos de los problemas que mencionamos al principio.
Fíjate que si hiciéramos la raíz cuadrada de ambos lados, la ecuación sería equivalente, quedando una expresión como la siguiente, que precisamente da respuesta a ese tipo de cuestiones.
- ¿Cómo se utiliza entonces el “i”?
Como siempre, un ejemplo nos ayudará mucho:
√(-9) = √(9 × -1) = √(9) × √(-1) = 3 × √(-1) = 3i
Imagen: questgarden

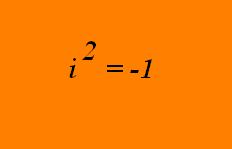
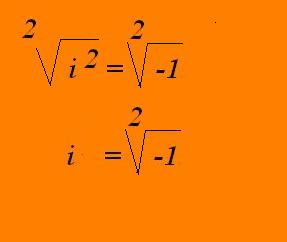




Corregir la multiplicación de “0,2 * 0,2 = 0,4” ya que en realidad, como bien sabes, es “0,04”
Gracias por tu observación, pues nos ayuda a mejorar nuestro trabajo. Quedó corregido el involuntario error de tipeo.
Saludos cordiales!