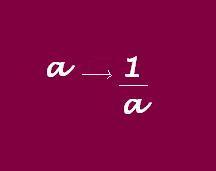El concepto o definición de números recíprocos, es muy sencillo de comprender y tiene más aplicaciones de las que puedas intuir en un primer momento. Te propongo aprender acerca de ellos, conocerlos un poco mejor y ejercitarte con diferentes propuestas.
Números recíprocos
Se denominan números recíprocos, aquellos que se relacionan entre sí cumpliendo la siguiente consigna: el producto (multiplicación) entre ellos es igual a 1. No necesariamente tienen que ser los números naturales, en este concepto se incluyen otros conjuntos numéricos siendo el caso mas claro el de los números racionales y el de los números decimales.
Expresado de otro modo: dos números a y b son recíprocos, si se cumple que
a * b = 1
Por ejemplo: es válido decir que el recíproco de 3, por ejemplo, es 1/3, porque
3 * 1/3 = 3/3 = 1
En términos generales, vale decir que
2· 1
2 = 1.
En general, el símbolo para el recíproco de un número cualquiera (llamémosle a) es siempre 1/a. Veámoslo en la siguiente imagen:
El concepto de número recíproco, es bien interesante para ejercitar tu razonamiento y pensamiento analítico; a veces con conceptos o propuestas muy sencillas, tales como la siguiente:
- Hallar el recíproco del número 12
12 * r = 1 => r = 1/12
Otros planteos exigen o mejor dicho, demandan un poco más de pensamiento. Por ejemplo podría ser un caso como este:
- p y q son números recíprocos. Sabiendo que p= 1/7… ¿cuál es q?
q es el recíproco de p, de modo que
q = 1/p
Otro tipo de consigna podría ser algo como lo siguiente:
- Prueba que dos números racionales, de la forma general a/b y b/a, son recíprocos entre sí.
La resolución de esta propuesta, pasa simplemente por aplicar la definición y multiplicarlos. Como sabemos, la multiplicación goza de propiedad conmutativa, por lo que numerador y denominador de la fracción racional resultante son iguales (a*b = b*a). Así las cosas, el cociente entre ambos números, da como resultado 1.
Veamos el proceso de razonamiento de la mano de la siguiente imagen:
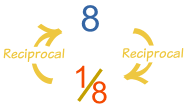
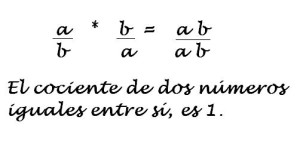¿Todos los números tienen su recíproco?
¿Te lo habías preguntado? Es una buena pregunta… y uno tiende a responderla rápidamente diciendo que sí, porque dado un número nos parece sencillo escribir el cociente 1/ese número.
Pero para responder pensando un poco mejor, debemos analizar la existencia de ese último planteo, es decir, pensar si hay algún caso en que el cociente 1/ “ese número” no exista, o esté matemáticamente indefinido.
Tal es el caso del cero. Decimos que el cero no tiene recíproco, porque 1/0 es lo que técnicamente se conoce como una indefinición matemática.
La respuesta a la pregunta, entonces, es no: no todos los números tienen su recíproco, el cero de hecho no lo tiene.
Imagen: pmeconsulting
