 Te invito a pensar, analizar y aprender acerca de las posiciones relativas entre rectas en el plano. Antes aprendimos y dejamos bien claras las definiciones y diferencias entre los conceptos de recta, semirrecta y segmento.
Te invito a pensar, analizar y aprender acerca de las posiciones relativas entre rectas en el plano. Antes aprendimos y dejamos bien claras las definiciones y diferencias entre los conceptos de recta, semirrecta y segmento.
Pero hay más: el análisis de casos de las posiciones relativas entre rectas del plano, nos devuelve cuatro casos diferentes de los que daremos cuenta a continuación. Te invito a pensarlos con cuidado, tomar nota y observar cada caso con la ayuda de las figuras con las que acompañamos cada uno de ellos.
Posiciones relativas entre rectas
Partiremos de las posiciones relativas entre rectas partiendo de dos de ellas consideradas en un mismo plano. Veamos cuáles son estas cuatro posiciones:
- Rectas paralelas
Es el caso de dos rectas cuyos puntos equidistan siempre, es decir los infinitos puntos de una de ellas están a la misma distancia de sus correspondientes de la otra. De ese modo, podemos afirmar que dos rectas paralelas, no se cortan nunca entre sí: por mucho que las recorras en un sentido y en otro, ellas no tienen ningún punto en común. Esto se debe a que dos rectas paralelas, sostienen siempre la misma dirección.
Te invito a observar la siguiente figura para comprender a fondo el concepto:
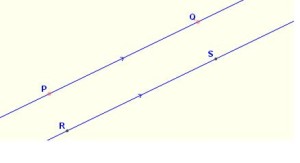 Como puedes apreciar, ambas rectas tienen la misma dirección y todos sus puntos equidistan respectivamente. Estas rectas no tienen ningún punto en común y nunca se van a cruzar.
Como puedes apreciar, ambas rectas tienen la misma dirección y todos sus puntos equidistan respectivamente. Estas rectas no tienen ningún punto en común y nunca se van a cruzar.
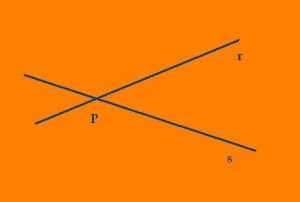
- Rectas secantes
Las rectas secantes son el caso opuesto al anterior; son dos rectas que pertenecen a un mismo plano, pero poseen direcciones diferentes por lo que en un punto u otro a lo largo de su infinita extensión se van a cortar. Dos rectas secantes, entonces, son aquellas que tienen un punto en común.
- Rectas perpendiculares
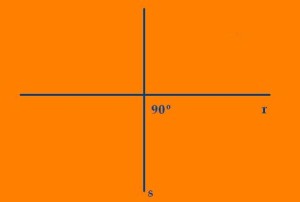
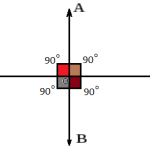
Si dos rectas, además de ser secantes, se cruzan entre sí formando un ángulo de 90º (vale decir un ángulo recto) son dos rectas perpendiculares. Queda claro que dos rectas perpendiculares tienen diferentes direcciones.
Observa la siguiente figura, donde queda claro el concepto y la imagen visual correspondiente a este caso:
Las rectas r y s, de la figura anterior, se cruzan en un único punto formando cuatro ángulos rectos. Este es el caso de dos rectas perpendiculares. Recuerda que siempre que hablemos de rectas, hablamos de conjuntos de puntos infinitos, por lo que las rectas no “empiezan” ni “terminan” por más que a los efectos del dibujo haya que darles un principio y un fin.
- Rectas coincidentes
Son aquellas que tienen todos sus puntos en común. Es una definición válida si lo piensas de esta manera:
- dos rectas paralelas son aquellas que no tienen ningún punto en común entre sí
- dos rectas secantes son aquellas que tienen un sólo punto común entre sí (al igual que sucede en el caso de las rectas perpendiculares)
- dos rectas coincidentes son aquellas que tienen todos sus puntos comunes entre sí.
Si las fuéramos a dibujar sería algo confuso, pues visualmente apreciarías una sola recta, pero conceptualmente hablaríamos de dos ya que todos sus puntos son coincidentes. Queda claro que dos rectas coincidentes tienen la misma dirección.
Imágenes: mathopenref; math