Continuamos compartiendo problemas que se resuelven con conjuntos. Créeme que se trata de una actividad que no sólo puede ser muy útil, sino que realmente llegarás a disfrutarla.
En un post anterior que titulamos Problemas acerca de conjuntos , habíamos dejado al “problema 3” planteado como desafío para que pudieras practicar las habilidades y conceptos que fuimos trabajando en otros post anteriores tales como Teoría de conjuntos y Unión e intersección de conjuntos .
¿Intentaste resolverlo por ti mismo? ¿Lo habrás hecho bien? Veamos cómo te has desempeñado en este nuevo desafío que forma parte de nuestra propuesta de…
Problemas que se resuelven con conjuntos
Ante todo, compartimos nuevamente la letra del problema en cuestión:
- Problema 3
En una celebración de graduación, las 30 estudiantes del curso debatían acerca de la bebida que debía servirse. Finalmente se optó por dos bebidas: cóctel de frutas sin alcohol y zumo de naranjas.Sabemos que…
-20 personas bebieron cóctel de frutas sin alcohol
-10 personas bebieron zumo de naranjas
-8 no concurrieron
Lo que queremos saber, es ¿cuántas de las personas que concurrieron, se sirvieron de las dos bebidas?
Procedimiento de resolución
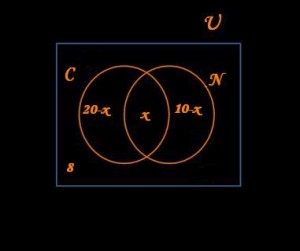
Te conviene disponer en esta ocasión, dos diagramas de Venn contenidos (como siempre) en un rectángulo “universo”. Al primero de los conjuntos le llamaremos C (por cóctel) y al segundo de ellos le llamaremos N (por naranja) y ambos se interceptan, es decir, habrá un espacio donde contener precisamente lo que es la incógnita de este problema, vale decir cuántas personas se sirvieron ambas bebidas. A este número de personas, por ser nuestra incógnita, le llamaremos “x”.
Es importante definir desde el principio cómo le llamaremos a la incógnita, pues habrá que restarla a los datos que nos da el problema, es decir a las 20 personas que sabemos certeramente que bebieron cóctel hay que restarle las que además bebieron zumo.
De este modo y con un razonamiento análogo para los que bebieron zumo (hay que restarle los que además bebieron cóctel), los sectores quedarían definidos de este modo:
- 20 – x = son las personas que bebieron cóctel pero no zumo
- x = son las personas que bebieron cóctel y zumo
- 10 – x = son las personas que bebieron zumo pero no cóctel
Por fuera de los diagramas de Venn, pero formando parte del “universo” hay que ubicar las 8 personas que no asistieron a la celebración.
Queda más claramente expresado, a través del siguiente diagrama de Venn:
problemas conjuntos
Como siempre, el paso siguiente, es expresar todo lo antes razonado a través de una ecuación. En este caso, tenemos claro que la totalidad de personas antes señalada y analizada, suma un total de 30, por lo que esta sería la ecuación que debemos plantear y su correspondiente resolución:
(20 – x) + x + (10 – x) + 8 = 30
20 – x + x + 10 – x + 8 = 30
38 – x = 30
– x = 30 – 38
– x = – 8
x = 8
La respuesta final a nuestro problema, es que son 8 las personas que bebieron ambas cosas, vale decir, cóctel de frutas sin alcohol y zumo de naranja.
Imagen: classroomclipart
