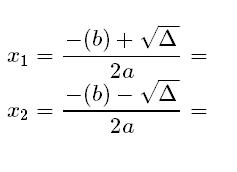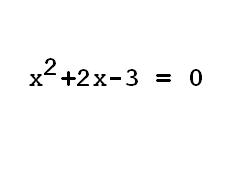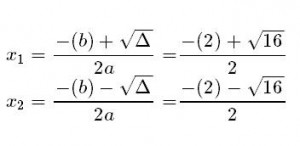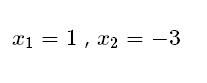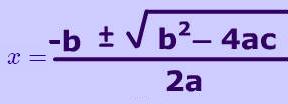¿Estás necesitando ayuda para resolver ecuaciones cuadráticas paso a paso? ¡Has llegado al lugar indicado! Comenzaré dándote una guía general (paso a paso, por supuesto) y luego aplicaremos esa misma guía a un ejemplo en concreto.
¿Estás necesitando ayuda para resolver ecuaciones cuadráticas paso a paso? ¡Has llegado al lugar indicado! Comenzaré dándote una guía general (paso a paso, por supuesto) y luego aplicaremos esa misma guía a un ejemplo en concreto.
Trabajar con ecuaciones cuadráticas o de segundo grado es muy sencillo: una vez que le tomas la mano y practicas lo suficiente, resolverlas se convierte en una rutina que no sólo es fácil sino que hasta la disfrutas, créeme. Siendo éste un tema básico con el que te cruzarás muchas veces en tu vida académica, te recomiendo que le prestes suma atención.
Cuando lo hayas comprendido, y creas que estás listo, puedes probarte a ti mismo: te desafío a trabajar con estos ejercicios de ecuaciones de segundo grado. Si no te satisfacen los resultados, trabaja nuevamente con los pasos que te aporta la siguiente guía, resuelve más ejemplos hasta que te sientas bien seguro y confiado al
Resolver ecuaciones cuadráticas paso a paso
- Aquí van los pasos generales:Identifica los coeficientes de la ecuación de segundo grado o cuadrática. Esto es, debes escribir y tener bien claro quienes son son a, b y c. Te recomiendo escribirlos de este modo (que incluye dejar anotado al opuesto de b, es decir -b, a quien necesitarás más adelante para la fórmula de resolución).
a=…
b=… -b=…
c=… - Calcula el discriminante. Como recordarás, llamamos discriminante al valor que está debajo del radical de la fórmula de resolución. Hablamos de Δ=b2−4ac
- Analiza el resultado de ese discriminante. Ese resultado te dará la pista para saber si la ecuación tiene una, dos o ninguna solución en el campo de los números reales. Esto lo sabrás, según el discriminante sea mayor, igual o menor a cero.
- Usa la fórmula cuadrática para obtener las mencionadas soluciones.
- Simplifica las soluciones si es posible y finaliza la resolución explicitando claramente la o las soluciones halladas, incluso si la ecuación no tuviera soluciones reales.
Ejemplo de resolución de una ecuación cuadrática
Se trata de aplicar los pasos señalados anteriormente, a un ejemplo concreto.
La ecuación que queremos resolver en este caso es la siguiente:
- Identificar los coeficientes
a=1
b=2 -b=-2
c=3 - Calcula el discriminante, vale decri: Δ=b2−4ac
En este caso, Δ= b2−4ac= (2)2−4(1)(−3)=16
- Analizar el resultado de ese discriminante. En este caso, el discriminante ha sido 16, esto es: discriminante mayor que cero. Cuando el discriminante es mayor que cero, inmediatamente podemos aseverar que esta ecuación tiene dos raíces o soluciones diferentes y pertenecientes al conjunto de los números reales.
- Usar la fórmula cuadrática para obtener las mencionadas soluciones. Para este ejemplo, esto quedaría planteado de la siguiente forma:
- Por último, hemos de realizar las operaciones correspondientes y simplificaciones en caso que corresponda con el objetivo de llegar a determinar cuánto valen las respectivas soluciones (recordarás que en el paso en que analizamos el discriminante, ya determinamos que serán dos, distintas y pertenecientes al conjunto de los números reales. El resultado de las mismas en este caso, es el siguiente.
Imagen: educationcreations.com