Antes de explicarte como se hace una suma de vectores por componentes hay que definir brevemente qué es un vector.
Un vector es una cantidad que tiene magnitud y dirección, ahora si que ya sabemos lo que es, podemos realizar suma de vectores por componentes.
Suma de vectores por componentes
Para sumar por componentes necesitamos saber los componentes en “x” y en “y” de cada vector, para esto se hace el siguiente proceso:
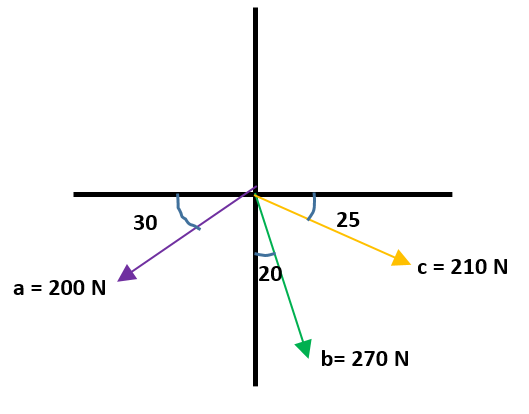
a = 100 N
b = 70 N
c= 50 N
d = 35 N
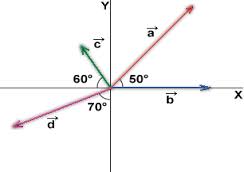
Primero sacamos los ángulos de cada vector al eje “x” positivo.
θ a =50°
θ b = 0°
θ c = 180 – 60 = 120°
θ d = 270 – 70 = 200°
Ahora sacamos las componentes en “x”
ax = 100N (cos 50°) = 64.28 N
bx = 70N (cos o°) = 70 N
cx = 50N (cos 120°) = -25 N
dx = 35N (cos 200°) = -32.89 N
Ahora sacamos las componentes en “y”
ay = 100N (sen 50°) = 76.6 N
by = 70N (sen o°) = 0 N
cy = 50N (sen 120°) = 43.3 N
dy = 35N (sen 200°) = -11.97 N
**Este método tiene la ventaja de sumar o restar dos o más vectores a la vez.
Ahora sumamos las componentes en “x” y en “y”
a+b+c+d = <76.39, 107.93>
El vector resultante tiene una magnitud de 132.22 N positiva.
Para saber la dirección de un vector se necesita un sistema de referencia, el más común es en donde “x” a la izquierda y “y” hacia abajo es negativo.
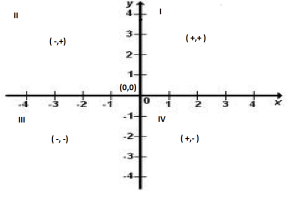
“x” es negativa si está a la izquierda del eje “y”.
“y” es negativa si está abajo del eje “x”.
Propiedades de la suma de vectores
- Asociativa u+ ( v + w ) = ( u + v ) + w
- Conmutativa w + v = v + w
- Elemento opuesto w + (−w ) = 0
- Elemento neutro v + 0 = v
Espero este artículo te haya sido de gran ayuda, ya vez ahora que es muy sencillo sumar vectores por este método!