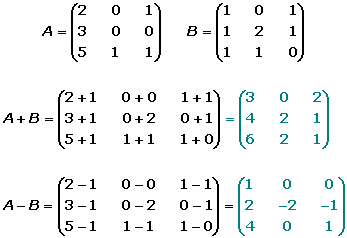
Dentro de las operaciones con matrices existen tres: Suma, Resta y multiplicación.
Empezaremos con Suma y Resta para poder entrar ya mejor a multiplicación después.
Suma y Resta de Matrices
Para poder sumar o restar matrices es necesario que se cumpla con las siguientes condiciones:
- Que las matrices a sumar o restar tengan el mismo tamaño.
- Que se suman o se restan los términos correspondientes de su posición.
Conociendo las condiciones ya podemos operar nuestras matrices.
Ejemplo:
1. Realice la suma de la Matriz A+ Matriz B y la resta Matriz B – Matriz A
A B
[2 4 9] [4 5 2 ]
[7 8 2] [3 9 11]
[3 1 0] [1 2 1 ]
Conociendo nuestras matrices y viendo que si se cumple la primera condición ,que es que las matrices son del mismo tamaño, pasamos a cumplir la segunda y sumamos los números según su posición.
A+B=
[(2+4=6) (4+5=9) (9+2=11) ]
[(7+3=10) (8+9=17) (2+11=13)]
[(3+1=4) (1+2=3) (1+0=1) ]
Entonces nuestra matriz resultante de la suma de A+B nos queda:
A+B =
[6 9 11]
[10 17 13]
[4 3 1 ]
Para resolver B-A aplicamos el mismo proceso, si nuestras matrices son del mismo tamaño procedemos a nuestra siguiente condición y tenemos:
B-A=
[(4-2=2) (5-4=1) (2-9=-7) ]
[(3-7=-4) (9-8=1) (11-2=9) ]
[(1-3=-2) (2-1=1) (1-0=1) ]
Por tanto nuestra matriz resultante de B-A nos queda:
B-A=
[2 1 -7]
[-4 1 9]
[-2 1 1]
2. Realice la suma de la Matriz A+Matriz B+Matriz C y la resta Matriz B – Matriz C + Matriz A.
A B C
[7 2 1] [8 6 4 ] [7 15 6]
[2 5 1] [2 1 10] [3 1 9]
[8 1 0] [7 3 5 ] [6 7 4]
Igual que en el ejercicio anterior al identificar que nuestras matrices si cumplen con la condición de ser del mismo tamaño empezamos a operar y tenemos:
A+B+C=
[(7+8+7=22) (2+6+15=23) (1+4+6=11) ]
[(2+2+3=7) (5+1+1=7) (1+10+9=20)]
[(8+7+6=21) (1+3+7=11) (0+5+4=9) ]
Por consiguiente nuestra matriz resultante de la suma de A+B+C nos queda:
A+B +C=
[22 23 11]
[7 7 20]
[21 11 9 ]
Ahora, para resolver B-C+A aplicamos el mismo proceso, solo aquí cuidando bien que números suman y restan para evitar cometer errores, entonces si nuestras matrices son del mismo tamaño procedemos a nuestra siguiente condición y tenemos:
B-C+A=
[(8-7+7=8) (6-15+2=-7) (4-6+1=-1) ]
[(3-2+2=3) (1-1+5=5) (10-9+1=2) ]
[(7-6+8=9) (3-7+1=-3) (5-4+0=1) ]
Por lo tanto nuestra matriz resultante de B-C+A nos queda:
B-C+A=
[8 -7 -1]
[3 5 2]
[9 -3 1]
Más ejercicios:
3. Realice la suma de la Matriz B+Matriz A y la resta Matriz A – Matriz B
A B
[7/2 15/4 6/5] [-2/3 -1/2 7/4 ]
[3 1/4 9/2] [4/3 -1/4 -9/2]
[6 7 4/3] [2 -1 -1/3 ]
4. Realice la suma de la Matriz A+Matriz B+Matriz C y la resta Matriz C – Matriz A + Matriz B.
A B C
[7 3 -1] [5 -13 0] [-3 5 9 ]
[4 -5 11] [2 20 5] [4 4 5 ]
[8 12 16] [7 2 1] [6 -9 14]
5. Realice la suma de la Matriz A+Matriz B y la resta Matriz B – Matriz A
A B
[10 11 3 5] [7 2 2 1 ]
[6 -9 0 4] [-1 7 11 19]
[4 0 12 6] [4 8 1 12]