Teorema del coseno ejemplos

Para terminar el estudio del Teorema del coseno ejemplos te servirán para poder comprender el tema en su totalidad.

El Teorema de los cosenos se puede aplicar de forma directa para calcular las partes restantes de un triángulo oblicuo (Triángulo que no contiene un ángulo recto), cuando se tiene cualquiera de los dos siguientes:

• Dos lados y el ángulo entre ellos
• Los tres lados

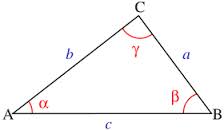
El teorema de los cosenos es el siguiente:

1. a² = b² + c² – 2bc cos α
2. b² = a² + c² – 2ac cos β
3. c² = a² + b² – 2ab cos ϒ

Teorema del coseno ejemplos

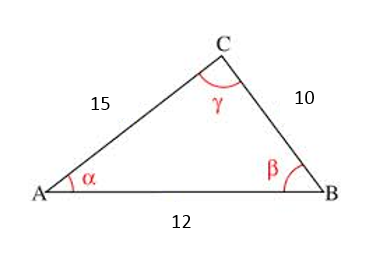
En los siguientes ejemplos calcularemos las partes restantes del triángulo ABC a partir de los siguientes datos utilizando el Teorema del coseno:

1. ϒ = 45°, b = 10, a = 15

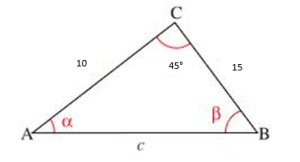
c² = a² + b² – 2ab cos ϒ

c² = 15² +10² – 2(15)(10) cos 45

c = 10.62

a² = b² + c² – 2bc cos α

15² = 10² + 10.62² – 2(10)(10.62 cos α

15² – 10² – 10.62² = – 2(10)(10.62) cos α

(15² – 10² – 10.62² )/ – 2(10)(10.62) = cos α

α = 93.3°

b² = a² + c² – 2ac cos β

10² = 15² + 10.62² – 2(15)(10.62) cos β

10² – 15² – 10.62² = – 2(15)(10.62) cos β

(10² – 15² – 10.62² )/ – 2(15)(10.62) = cos β

β = 41.7°

2. β = 73°50′, a = 87, c = 14

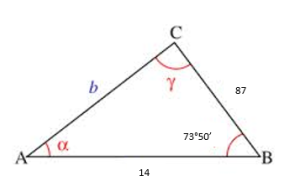
b² = a² + c² – 2ac cos β

b² = 87² + 14² – 2(87)(14) cos 73°50′

b = 84.18

c² = a² + b² – 2ab cos ϒ

14² = 18² + 84.18² – 2(87)(84.18) cos ϒ

¹⁴² – 87² – 84.18² = – 2(87)(84.18) cos ϒ

(14² – 87² – 84.18² )/– 2(87)(84.18) =  cos ϒ

ϒ = 9.2°

a² = b² + c² – 2bc cos α

87² = 84.18² + 14² – 2(84.18)(14) cos α

87² – 84.18² – 14² =– 2(84.18)(14) cos α

(87² – 84.18² – 14² )/ – 2(84.18)(14) = cos α

α = 96.98°

3. a= 25′, b= 80, c= 60

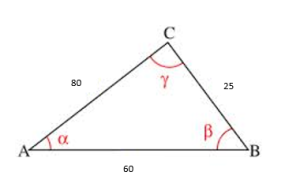
a² = b² + c² – 2bc cos α

25² = 80² + 60² – 2(80)(60) cos α

25² – 80² – 60² =– 2(80)(60) cos α

(25² – 80² – 60² )/ – 2(80)(60) = cos α

α = 12.43°

b² = a² + c² – 2ac cos β

80² = 25² + 60² – 2(25)(60)cos β

80² – 25² – 60² =– 2(25)(60)cos β

(80² – 25² – 60² )/ – 2(25)(60)=cos β

β = 136.47 °

c² = a² + b² – 2ab cos ϒ

60² =25² + 80² – 2(25)(80) cos ϒ

60² – 25² – 80² = – 2(25)(80) cos ϒ

(60² – 25² – 80² )/– 2(25)(80) =  cos ϒ

ϒ = 31.10°

4. a = 20, b = 20, c = 10

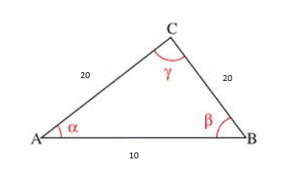
a² = b² + c² – 2bc cos α

20² = 20² + 10² – 2(20)(10)cos α

20² – 20² – 10² =– 2(20)(10)cos α

(20² – 20² – 10² )/– 2(20)(10) =cos α

α = 75.52°

b² = a² + c² – 2ac cos β

20² = 20² + 10² – 2(20)(10)cos β

20² – 20² – 10² = – 2(20)(10)cos β

(20² – 20² – 10² )/– 2(20)(10)cos =  β

β = 75.52°

c² = a² + b² – 2ab cos ϒ

10² =20² + 20² – 2(20)(20) cos ϒ

10² – 20²  – 20² = – 2(20)(20) cos ϒ

(10² – 20²  – 20² )/– 2(20)(20)=  cos ϒ

ϒ = 28.96°

Espero que con estos ejemplos te haya sido más claro el Teorema del coseno ejemplos! no olvides seguir practicando y nos vemos… hasta la próxima!