 Estudiar las transformaciones en el plano es simplemente fascinante, pues hablamos de aprender a trabajar con figuras convexas o cóncavas en el plano, transformándolas de diversas maneras sin alterar su esencia.
Estudiar las transformaciones en el plano es simplemente fascinante, pues hablamos de aprender a trabajar con figuras convexas o cóncavas en el plano, transformándolas de diversas maneras sin alterar su esencia.
No existe un único tipo de transformaciones en el plano, por lo que antes de entrar en detalle en cada una de ellas, aprenderlas y ejercitarlas comenzaremos por clasificarlas y comprender las diferencias entre ellas. Más tarde, en otros post, te invitaré a conocer a cada una con mayor profundidad.
Transformaciones en el plano
Una de las clasificaciones más utilizadas, pero a la vez más sencillas de comprender cuando hablamos de transformaciones en el plano, es la que divide a las mismas en transformaciones isométricas y transformaciones no isométricas en el plano.
Te propongo comenzar por analizar la palabra isometría, que proviene de la fusión de dos palabras griegas que son las siguientes: iso (que significa igual o “lo mismo”) y metría (que significa medida o medir).
Basándonos en este significado, es que podemos decir que:
- Transformaciones isométricas en el plano, son aquellas que mantienen la forma y el tamaño de la figura en cuestión, vale decir no se altera la longitud de sus lados (si hablamos de un polígono) ni otras medidas claves (como el radio si hablamos de una circunferencia).
- Transformaciones no isométricas en el plano, son aquellas que -por el contrario- alteran una o más de las dimensiones de las figuras. Por ejemplo, un caso muy frecuente es que a consecuencia de una transformación, se varíe proporcionalmente el tamaño de los lados y en consecuencia la superficie.
Transformaciones isométricas en el plano
Como ya señalamos son aquellas que a pesar de someter a la figura en cuestión a algún tipo de desplazamiento en el plano, mantienen las medidas y forma de la figura. Las transformaciones de este tipo que se estudian a nivel del plano, son básicamente tres:
- Traslación
- Rotación
- Simetrías
Vale señalar que en algunos cursos escolares, la última de las transformaciones en el plano mencionadas, la simetría, también es conocida o mencionada como reflexión (por “reflejo”, aludiendo a las imágenes “espejo” que resultan en algunos casos particulares). Por otra parte, escribimos simetrías (en plural) porque como veremos más adelante, existen distintos tipos de simetrías que estudiaremos con mayor detalle, tales como la simetría axial o la simetría central.
Transformaciones isométricas en el plano
Como hemos señalado antes, en este caso hablamos de aquellas transfomaciones que al someter a la figura en cuestión a algún tipo de desplazamiento en el plano, altera una o más de las medidas de la misma.
La más común de estas transformaciones en el plano que se estudia en los cursos escolares es la
- Homotecia
Imágenes de transformaciones en el plano
Veamos a continuación algunos ejemplos de figuras que representan estas transformaciones en el plano, aclarando que dedicaremos algunos post a estudiar a cada una de ellas con mayor detalle.
Presta atención: comienzo por las transformaciones isométricas es decir aquellas que no alteran medidas ni dimensiones:
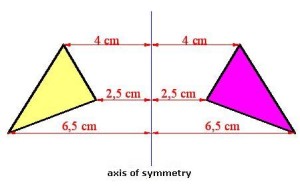
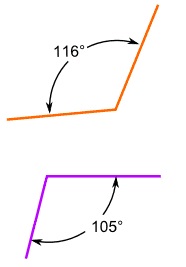
- Simetría axial
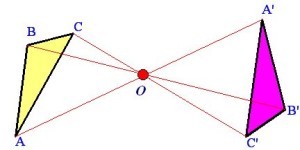
- Simetría central
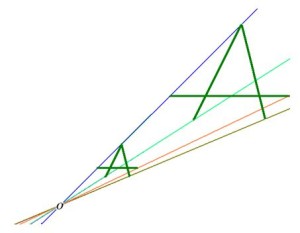
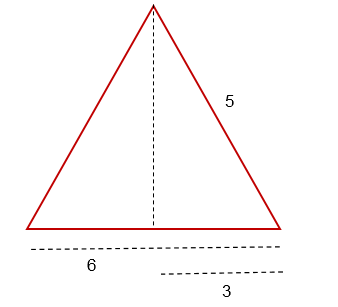
- Homotecias
Imágenes: easycoursesportal



No hay respuetas