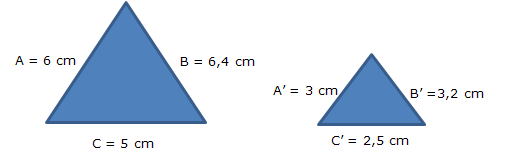Lee con atención el siguiente enunciado: Dos Triángulos son Semejantes cuando sus ángulos son respectivamente iguales y sus lados homólogos sean proporcionales.
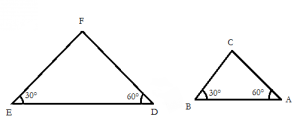
Observa la Siguiente Figura:
¿Qué notas?
Es muy probable que hayas contestado: Se parecen pero uno es más grande que el otro.
Bien, si contestaste eso, eres un gran observador pues cuando dos objetos o figuras son iguales pero de distintos tamaños podemos decir que son “semejantes”.
A Continuación, trataré de explicar aquellas palabras que forman parte de la definición de Triángulos Semejantes para que lo entiendas perfectamente bien.
Si has podido estudiar el tema correspondiente de razones y proporciones, es posible que hayas encontrado que una figura geométrica es proporcional a otra cuando la figura más grande “cabe” un cierto número de veces dentro de la otra.
Observa la siguiente figura:
Nota que ambas se parecen, tienen los mismos lados pero la figura más grande tiene sus lados tres veces más grandes que la otra. Esto lo sabemos ya que si multiplicamos cada uno de los lados de la figura pequeña por 3, nos da como resultado el valor de los lados de la figura grande.
A esto se le llama proporción y entonces podemos decir que una figura es proporcional a otra un cierto número de veces, en nuestro ejemplo entonces, la figura A es tres veces proporcional a la figura B.
Decimos que algo o alguien es homólogo, cuando ocupa el mismo lugar o cumple las mismas funciones que otra. Por ello cuando dos presidentes de un país se reúnen, algunos reporteros usan una frase como esta: “El presidente se reunió con su homólogo”.
Entonces, si volvemos a nuestra definición de semejanza, podemos explicarla un poco mejor: Dos triángulos son semejantes si sus ángulos son iguales y sus lados homólogos son iguales. Es decir, que si los lados del otro triángulo que van con los ángulos iguales son proporcionales, entonces podemos decir que los dos son Triángulos Semejantes.
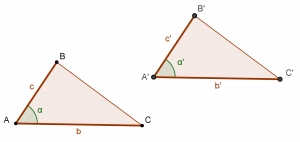
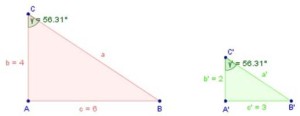
Observa la siguiente figura:
Como puedes notar el primero es dos veces más grande que el segundo y sus ángulos son exactamente iguales, por lo tanto son Triángulos Semejantes.
Criterios de Semejanza.
Seguramente ya tuviste oportunidad de estudiar los temas referentes a Congruencia de Triángulos, en esos temas explicamos los llamados Criterios de Congruencia que nos permiten saber a partir de pocos elementos, cuáles son Iguales y cuáles no.
También tenemos Criterios de semejanza de Triángulos y son lo siguientes:
Criterio Lado, Ángulo, Lado (LAL): Dos Triángulos que tienen dos lados proporcionales y el ángulo entre ellos iguales son semejantes entre sí.
Criterio Ángulo, Ángulo (AA): Dos Triángulos que tienen dos ángulos respectivamente iguales, son semejantes.
Criterio Lado, Lado, Lado (LLL): Dos Triángulos que tienen tres lados respectivamente proporcionales son semejantes entre sí
Criterio Lado, Lado, Ángulo (LLA):Dos Triángulos que tienen dos de sus lados respectivamente proporcionales y el ángulo opuesto al mayor de ellos son semejantes.
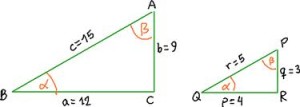
Criterios de Semejanza de Triángulos Rectángulos.
Aunque los criterios de Semejanza anteriores aplican para cualquier tipo de Triángulo, aquí te presento algunos criterios para el Triángulo Rectángulo:
Dos Triángulos Rectángulos que tienen sus catetos proporcionales, son semejantes.
Dos Triángulos Rectángulos que tengan un ángulo agudo igual, son semejantes.
Dos Triángulos Rectángulos que tienen la hipotenusa y su par de catetos proporcionales, son semejantes.