La unión e intersección de conjuntos son las operaciones más reconocidas y utilizadas, en relación a la teoría de conjuntos. En base a ellas, combinándolas o no, resolverás algunas situaciones problemáticas que de otro modo serían realmente complejas.
De la mano de otros dos conceptos clave, Conjunto vacío y subconjuntos, tendrás la posibilidad de analizar las consignas que se te planteen y arribarás a las respuestas pedidas en cada caso. Veamos las correspondientes definiciones y ejemplos de la…
Unión e intersección de conjuntos
- ¿Qué significa unir dos o más conjuntos?
La operación se denomina unión de conjuntos, y da como resultado un nuevo conjunto formado por todos los elementos que pertenecen a ambos conjuntos. Escrito con símbolos, la unión de dos conjuntos (por ejemplo llamados G y H) se denota así:
G ∪ H
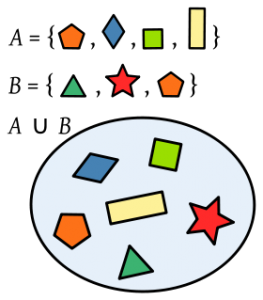
Si queremos expresarlo en diagramas de Venn, deben primero representarse todos los elementos en sus respectivos conjuntos y luego incluyen todos (sin repetirlos) en un mismo diagrama. En la siguiente imagen, se puede apreciar esta definición con mucha claridad. Presta atención:
- ¿Qué es intersección de conjuntos?
Realizar la intersección de dos o más conjuntos, es definir un nuevo conjunto formado solamente por aquellos elementos que estén presentes en todos los conjuntos en cuestión. En otras palabras: sólo forman parte del nuevo conjunto, los elementos que tengan en común.
Existe un símbolo matemático para la intersección. Para poner un ejemplo,la intersección de dos conjuntos llamados G y H se denota de la siguiente manera:
G ∩ H
En vez de ejemplificar en diagramas, esta vez veremos cómo se representa la interescción de conjuntos definida por extensión.
Primero definimos a los respectivos conjuntos:
G = { a, b, c, d, e, f, g, h }
H = { a,e,i,o,u }
G ∩ H = { a,e }
En efecto, a y e, son los únicos elementos en común, es decir que están presentes en los dos conjuntos a la vez.
Veamos un ejercicio ejemplo:
Partimos de la existencia de dos conjuntos que son los siguientes:
R = {–7–2, 0, 2, 4}
S = {–4, –2, 5, 3, 4}
Se pide realizar las siguientes operaciones:
a) R ∪ S
b) R ∩ S
a) que la unión de conjuntos se plantea como la reunión de los elementos de ambos conjunto, sin escribir repetidos los que están dos veces. Entonces quedaría que:
R ∪ S = {–7–2, 0, 2, 4, –4, 5, 3}
b) Recordamos que la intersección de conjuntos, se plantea como la lista de elementos que ambos tienen en común. Entonces, en este caso, quedaría que:
R ∩ S = {–2, 4}
- Caso especial: conjuntos disjuntos
Podría ser que al intentar realizar la intersección de conjuntos, éstos no tengan elementos en común. En ese caso, se dice que la intersección es vacía, o sea, es un conjunto vacío. Escrito en símbolos, esto se señala así:
A ∩ B = ∅
De la mano de esto, introducimos un nuevo concepto: el de conjuntos disjuntos. Se dice que dos conjuntos son disjuntos, cuando su intersección es vacía. Para citar un ejemplo podríamos decir que si C, es el conjunto de las letras consonantes y V es el conjunto de las letras vocales,
C ∩ V = ∅
Imágenes: es.wikipedia
