Comienzo por decirte que el título volumen de cuerpos en el espacio, es en sí mismo toda una redundancia ya que estamos hablando de dos conceptos que están estrechamente relacionados entre sí.
Para ser más clara, lo pondré de esta forma:
- Defino al concepto de volumen, como el espacio que ocupa un cuerpo.
- Defino al concepto de cuerpo, como todo objeto que ocupa un lugar en el espacio.
Calcular cuál es ese volumen, no siempre es sencillo, todo depende de qué tipo de cuerpo estamos hablando: si tiene una cierta regularidad geométrica (un prisma recto, un cilindro, un cubo etc) será sencillo hacerlo a través de fórmulas. Si no fuera ese el caso (imagina el caso de un juguete de plástico), ya no es tan fácil, por lo que podrías recurrir a un viejo truco, muy efectivo. ¿Sabes cuál es? Tomas un recipiente en el cual quepa el objeto en cuestión (un vaso si es algo pequeño, un balde si fuera algo más grande) y lo llenas al ras de agua. Luego sumerges el objeto del cual quieres calcular el volumen y recoges cuidadosamente la cantidad de agua que éste desplaza al ser sumergido. Luego simplemente mides cuánto es el volumen de esa agua y ya tienes tu respuesta.
Pero en matemáticas, nos concentraremos en aquellos cuerpos geométricos más usuales, y será sobre ellos que trabajaremos el concepto de
Volumen de cuerpos en el espacio
Podemos decir como pauta general, que para hallar el volumen de un cuerpo en el espacio, hay que multiplicar sus tres dimensiones, y de allí resultará el valor final expresado en unidades de volumen. Te invito a repasar este concepto en un post anterior, que titulamos ejercicios de unidades de volumen.
Dicho de otra forma, en la mayoría de los casos, para hallar el volumen de un cuerpo geométrico (tal como un prisma, o un cilindro), habrá que calcular la superficie de su base (las dos primeras dimensiones) y multiplicarla por su altura (se incorpora la tercera dimensión).
Ejemplo de cálculo de volumen
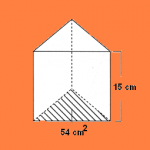
Observa con atención la figura de portada. Se nos pide calcular su volumen.
Está claro que el cálculo partirá de multiplicar la superficie de la base (que ya está expresada en la figura como 54cm2) por la altura (15 sm). La operación total, entonces, quedaría resumida en los siguientes planteos:
Vol = sup. de la base * altura
Vol = 54 cm2 * 15 cm
Vol = 810 cm3
Veamos otro ejemplo; se trata de un prisma de base cuadrada cuyas medidas están especificadas en la siguiente figura.
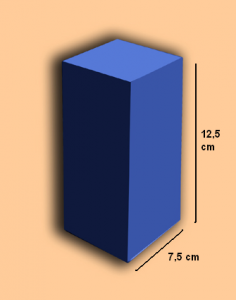El cálculo para su volumen no difiere del caso anterior, es decir, será superficie de la base multiplicado por la altura. Veamos cómo quedaría el planteo:
Vol = sup. de la base * altura
Sup de la base = 7,5 cm * 7,5 cm = 56,25 cm2
Vol = 56,25 cm2 * 12,5 cm
Vol = 703,125 cm3
Por último, veamos el caso del cálculo de volumen de un cilindro recto. El volumen se calcula bajo la misma idea, es decir superficie de su base multiplicada por su altura. En la siguiente imagen queda explicado cómo se realiza el cálculo de volumen, toma nota:
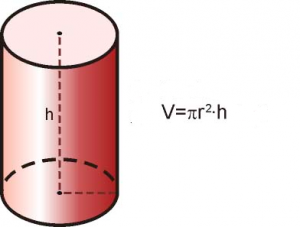Imagen: sehacesaber
