El estudio de los Ángulos ocupa gran parte de “Los Elementos”, la obra cumbre de Euclides, que ha formado el pilar de la geometría a través de gran parte de la Historia de la Humanidad; este es considerado uno de los libros de texto más divulgado en la historia, y el segundo en número de ediciones publicadas, después de la Biblia. Durante varios siglos, “El Quadrivium”, que era la forma de organización metodológica de la enseñanza, estaba incluido en el temario de los estudiantes universitarios.
Quadrivium significa “cuatro caminos”; agrupaba en sí, las disciplinas concernidas con las matemáticas, según la máxima Ar. numerat, la aritmética numera, Geo. ponderat, la geometría pondera, As. colit astra, la astronomía cultiva los astros, Mus. canit, la música canta; Arquitas de Tarento (c. 430 a. C.- c. 360 a. C.) fue un filósofo, matemático, astrónomo, estadista, general y contemporáneo de Platón, que sostuvo que la matemática estaba constituida por tales disciplinas también, el camino del desarrollo y relación entre estas disciplinas se comportaría entonces, según esta metodología.
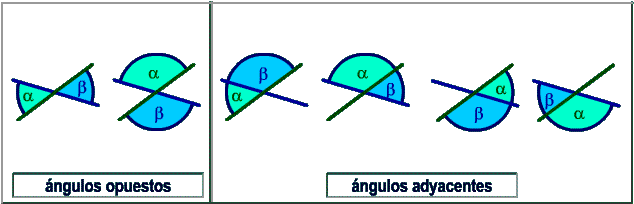
Ángulos opuestos:
En la geometría euclidiana básica, entender los ángulos opuestos es sólo el comienzo, y él definió a la línea como una longitud sin anchura, y también es una línea que descansa uniformemente en los puntos de sí misma, para Euclides un ángulo podía definirse como la inclinación mutua entre dos líneas, que se encuentran una a otra sobre un plano, y no están en línea recta, una con respecto a la otra (paralelas), sin embargo, algunos otros estudiosos desarrollaron otras definiciones como la de Proclo, quien consideró que un ángulo debe ser una calidad o una cantidad, o una relación.
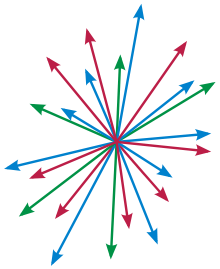
A las cuatro partes ilimitadas en las que queda dividido un plano cuando dos rectas se cortan, se le llama región angular y estas partes se miden de acuerdo a su área similtudinal. Cuando dos de estas líneas rectas se intersectan, forman cuatro ángulos, que, si son ángulos rectos, es decir, si son ángulos de 90 grados (4 ángulos rectos), las dos líneas son perpendiculares una de la otra.
Si dos líneas se intersectan sin formar ángulos rectos, estas líneas no son perpendiculares entre sí. En este caso, si tomamos un ángulo como referencia, es adyacente a dos de los otros ángulos y opuesto al restante. Funcionando de la misma forma si cambiamos el ángulo de referencia.
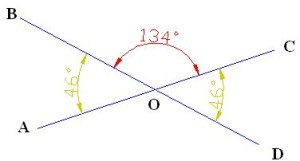
Los ángulos opuestos comparten sólo un punto y se encuentran directamente opuestos entre sí por la intersección de las dos líneas.
Ángulos opuestos y adyacentes:
Dos ángulos adyacentes siempre suman 180 grados. Si las dos líneas que se interceptan son perpendiculares, cada uno de los cuatro ángulos será equivalente a 90 grados. Dos ángulos adyacentes cualquiera sumarán siempre un total de 180. Si las dos líneas que se intersectan no son perpendiculares, cualquier par de ángulos adyacentes seguirán sumando un total de 180. Un ángulo será de más de 90 grados y el otro será de menos de 90. Un par de ángulos opuestos siempre son equivalentes.
Ahora que has visto las características y las bases de los ángulos opuestos, puedes practicar desarrollando ejemplos de ángulos opuestos con tus amigos y compañeros de estudio, recuerda que las matemáticas estánpresentes en todo lo que nos rodea, la geometría está en nuestras calles, en los objetos, en los alimentos, y hasta en nosotros mismos. Anímate a observar la geometría que te rodea.