 La comparación de fracciones es una operación a la que tendremos que enfrentarnos cuando menos lo pensamos. ¿Es difícil? Para nada, créeme. Como siempre distinguiremos los casos que se nos pueden presentar y aprenderemos a proceder en cada uno de ellos.
La comparación de fracciones es una operación a la que tendremos que enfrentarnos cuando menos lo pensamos. ¿Es difícil? Para nada, créeme. Como siempre distinguiremos los casos que se nos pueden presentar y aprenderemos a proceder en cada uno de ellos.
La mayoría de las veces necesitaremos comparar dos fracciones para descubrir cuál de ellas es más grande o cuál la más pequeña. Para no dar rodeos, comparto ya mismo las dos formas más sencillas y fáciles para hacer sin ningún problema una rápida…
Comparación de fracciones
Hay dos métodos bien fáciles para comparar fracciones, estos son:
- Uso de decimales
Usando el mismo denominador
- Uso de decimales
Es la forma más usual y consiste simplemente en realizar la división que en definitiva toda fracción está indicando (dividimos numerador entre denominador) y comparamos los decimales resultado.
Veamos un ejemplo:
¿Qué fracción es más pequeña, 3/8 ó 5 12? Al tratarse de fracciones de diferente denominador no es tan sencillo percibirlo así a primera vista…
Convertiremos entonces cada una de ellas a su correspondiente expresión decimal, a saber:
3/8 = 3÷8 = 0,375
5/12 = 5÷12 = 0,4166…
¿Verdad que es mucho más claro así? Sin ninguna duda decimos que como
0,375 < 0,4166 (0,375 es menor que 0,4166)
entonces
3/8 < 5/12 (3/8 es menor que 5/12)
- Usando el mismo denominador
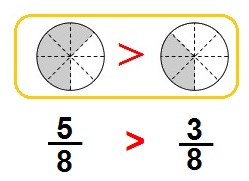
El principio que aplicamos aquí es que cuando dos fracciones tienen el mismo denominador, es muy fácil compararlas; por ejemplo está claro que 3/4 son más que 1/4.
Entonces, cuando queremos comparar dos fracciones que tienen distinto denominador, lo que podemos hacer es convertirlas en fracciones equivalentes que tengan igual denominador. Hecho esto, será muy sencillo y rápido determinar cuál es más grande y cuál es más pequeña.
Veamos el mismo ejemplo que usamos en el método anterior y apliquemos este método:
Queremos comparar 3/8 y 5/12
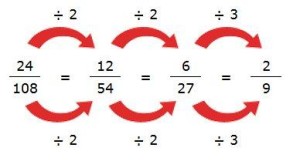
El múltiplo común más pequeño que comparten los denominadores 8 y 12 es 24. Tendremos que hallar las respectivas fracciones equivalentes multiplicando numerador y denominador de la primera por 3 y numerador y denominador de la segunda por 2.
3 3 9
__ * ___ = ___
8 3 24
5 2 10
__ * __ = __
12 2 24
Fíjate ahora que es mucho más sencillo visualizar que 9/24 es menos que 10/24; al igual que con el método anterior, queda claro que:
3/8 < 5/12 (3/8 es menor que 5/12)
Te propongo analizar otro ejemplo en el que aplicamos precisamente este segundo método. Supongamos que el reto es comparar las fracciones
5/6 y 13/15
Dado que son de diferente denominador, hemos de llevar cada una de ellas a una fracción equivalente pero que tengan un mismo denominador; en este caso elegimos llevar ambas a una fracción equivalente de denominador 30. El procedimiento que seguimos para obtenerlas se ilustra en la siguiente imagen:
La comparación es ahora muy sencilla: queda claro que 25/30 es menor que 26/30.
Imágenes: mathatube ; mathisfun