Congruencia de tríangulos: Se dice que dos triángulos son congruentes cuando son iguales tanto sus ángulos como sus lados.
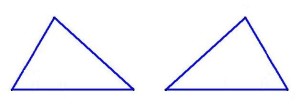
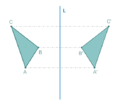
Observa la siguiente figura:
¿Qué notas?
Observa que ambos son exactamente iguales, la única diferencia es que ambos están como reflejados por un espejo ¿si lo ves?
Un triangulo es congruente cuando, sin importar la orientación, el largo de sus lados y el tamaño de sus ángulos son iguales, por lo que si consideramos que el triángulo de la derecha tiene lados abc y ángulos ABC y el de la izquierda tiene lados a’b’c’ y ángulos A’B’C’, podemos escribir la siguiente fórmula de Congruencia de Triángulos:
A=A’ y B=B’ y C=C’ y a = a’ y b=b’ y c=c’ (Nota que la y indica unión, es decir, que todas las igualdades deben cumplirse).
Cuando los triángulos que se comparan son pequeños y conocemos los valores de sus lados y sus ángulos es fácil decidir si son congruentes o no, pero cuando desconocemos algún dato o es difícil obtener la información (si se trata de dos terrenos muy grandes de forma triangular por ejemplo) podemos usar menos elementos para saberlo. Podemos por ejemplo medir tan sólo dos ángulos y un lado, o dos lados y un ángulo confirmando que sean iguales.
Criterios de Congruencia de triángulos.
Se llama o denomina criterio a una norma o regla que nos permite saber la verdad, es por ello que la norma o regla que nos permite saber de manera rápida si un triángulo es congruente o no se conoce como criterio de congruencia.
Cuando se cumplen los criterios de Congruencia al comparar dos triángulos, entonces podemos concluir que existe Congruencia de Triángulos.
Los Criterios que se utilizan para saber si la Congruencia de Triángulos existe es:
1. Lado, Lado y Lado (se abrevia L,L,L).
Observa la siguiente figura:
¿Qué ves?
Nota que hemos marcado cada uno de los lados iguales con un pequeño símbolo. Nota también que aunque los triángulos están en diferentes direcciones, si sus lados son iguales podemos entonces concluir que son congruentes. Es decir que hay una Congruencia de triángulos.
2. Lado, Ángulo, Lado (L,A,L).
Ahora observa esta figura:
¿Qué notas?
Nota que estamos comparando dos lados y el ángulo que se encuentra entre ellos, si son iguales, entonces podemos concluir que son congruentes o que hay una Congruencia de Triángulos.
- Ángulo, Lado, Ángulo (A, L, A).
Ahora, ve esta figura atentamente:
Nota que hemos tomado dos ángulos y el lado que se encuentra entre ellos y los hemos comparado, si este criterio se cumple entonces podemos concluir que existe Congruencia de Triángulos.
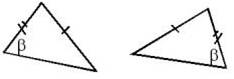
4. Lado, Lado, Ángulo (L, L, A)
Ahora. Observa esta figura, notarás algo distinto:
¿Qué es?
Hasta ahora los triángulos que hemos comparado han sido, dos lados y el ángulo entre ellos, dos ángulos y el lado entre ellos, pero en este caso, son dos lados y el ángulo opuesto mayor. Nota que en la figura anterior se ha escogido como comparación el ángulo mayor o que esta más abierto. Si se cumple este último criterio concluimos que existe Congruencia de Triángulos.
me gustaría comentarte para terminar este tema, que aunque parece poco importante, más adelante iremos descubriendo juntos la importancia de estas herramientas.


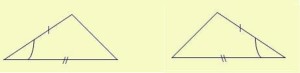
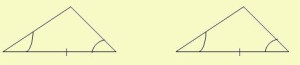



No hay respuetas