Conversión de ángulos

El tema no es para nada menor: he visto muchos buenos estudiantes perder sus exámenes por no dominar la conversión de ángulos, es decir  entre distintas formas de medición de ángulos.

Antes de ingresar en el tema en sí, te sugiero repasar los conceptos más básicos que ya compartimos cuando hablamos de grados, radianes y gradianes. De todos modos, el propósito de este post es conocer, reafirmar y ejercitar los fundamentos de la…

Conversión de ángulos

El tema es de suma importancia, y en ese sentido comienzo por decirte que es de suma importancia que tengas siempre a mano y sepas bien cómo usar la calculadora científica, tanto para ir comprobando y ejercitando sobre los ejemplos que citaremos en este post como para resolver todas las situaciones problemáticas y ejercicios vinculados a la trigonometría.

En relación a la conversión de ángulos, es importante recordar que en la calculadora científica, podemos ver ciertas abreviaturas que nos ayudan a la conversión de las Funciones Trigonométricas. Éstas son

• Grados sexagesimales (D) (DEG)
• Radianes (R) (RAD)
• Gradianes (G) (GRAD)

Comienzo por reiterar algunas conceptos básicos del sistema de medición más trabajado, esto es, los grados sexagesimales.

• 1 º es la forma de simbolizar un grado sexagesimal
• 1º = 60 minutos = 60′ (un grado se divide en 60 partes iguales, cada una de ellas se llama minuto)
• 1′ = 60 segundos = 60”  (un minuto se divide en 60 partes iguales, cada una de ellas se llama segundo)

Ahora bien, si lo que queremos es trabajar, son las equivalencias para ejercitar sobre las conversiones, un buen punto de partida es señalar que:

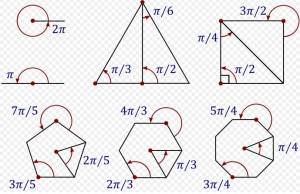
• Un ángulo de 180° equivale a π radianes
• Un ángulo de 360° equivale a 2π radianes
•  Vale recordar que el número π ≈ 3,14159265359…

En la siguiente imagen que tomamos de wikipedia, pueden observarse muy bien estas equivalencias:

 Algunos casos particulares

Por ejemplo, puede suceder que se nos presente el caso de tener que convertir una medida de ángulo expresada como decimal, a grados minutos y segundos. Lo mejor es analizar un ejemplo:

• Convertir 18, 4567º a grados, minutos y segundos.

La buena noticia, es que si dispones de una calculadora científica, una tecla especial de la misma (busca la que tiene juntos los símbolos º ‘ ”) hará todo el trabajo. Si no dispones de ella, esto es lo que debes hacer…

1) Se toma la parte entera y esos son grados netos, sin duda. Así que vamos contabilizando 18º.

2) Luego tomamos la parte decimal  la multiplicamos por 60, para obtener los minutos, así:  0.4567 * 60 = 27.402. De este resultado nuevamente separamos la parte entera, es decir 27, que serán los minutos.

3) Por último tomamos los decimales que no usamos en el paso anterior es decir los 0,402 y los multiplicamos nuevamente por 60, para obtener los segundos.  De este modo, obtenemos: 0.402 x 60 = 24.12. De este resultado, nuevamente se toma la parte entera despreciando la decimal.

Resultado final: 18, 4567º = 18 º 27 ‘ 24”

Conversión grados – radianes y viceversa

Por último, vamos a compartir dos fórmulas prácticas y un par de ejemplos.

• Si queremos convertir de radianes a grados, vamos a utilizar la siguiente fórmula:

Ejemplo: si te piden convertir 4,36 radianes a grados, la operación será: 180 (4,36) y luego dividido por 3,1416. El resultado será 249,8090145, que convertido serán 249º 48’32”.

• Si queremos convertir de grados a radianes, vamos a utilizar la siguiente fórmula:

Ejemplo: si te piden convertir 44º 47 ‘ a radianes, razonarás así:

60′ = 1º
47′ = x

Resolviendo esa regla de tres simple, obtienes x = 0,783333 que son los minutos expresados en grados, para sumarlos a los 44 que ya tienes y poder usar la fórmula anterior.

Entonces: harás 3,1416  * ( 44, 783333) dividido 180 y obtendrás 0,78 radianes.