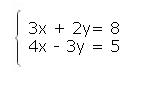Te propongo aprender hoy el tercero de los métodos de resolución de un sistema de ecuaciones simultáneas de primer grado, esto es el método de reducción. Si quieres repasar o practicar los que vimos anteriormente, aquí mismo te dejo vínculo al primero de los métodos algebraicos que vimos, el método de igualación y al segundo, esto es, el método de sustitución.
Este nuevo método para resolver un sistema de ecuaciones simultáneas, recibe el nombre de método de reducción, porque precisamente eso trataremos de hacer con las incógnitas comunes en ambas ecuaciones.
Como recordarás, a las ecuaciones simultáneas también se las llama sistemas de ecuaciones de primer grado y te propongo ver de inmediato en qué consiste este método utilizando – como hemos hecho en los casos anteriores-, un sistema de ecuaciones simultáneas de primer grado con dos incógnitas.
Toma nota y no tardarás en aprender el …
Método de reducción
En líneas generales, lo que buscamos al poner en marcha este método, es que mediante la multiplicación de cada ecuación, por un factor elegido convenientemente, los coeficientes de una misma incógnita sean números opuestos, es decir que al sumarlos, se anulen entre sí.
De este modo obtendremos una ecuación en una sola incógnita que resolveremos como lo hacemos habitualmente. Cuando tengamos ese valor, lo sustituimos en cualquiera de las ecuaciones para hallar la otra incógnita. Posteriormente verificamos los resultados obtenidos y ambas ecuaciones deberán probar que son igualdades.
Como habitualmente hacemos, te propongo resolver el sistema de ecuaciones simultánea que hemos tomado como modelo, esta vez aplicando el método de reducción. Paso a paso, como siempre.
El sistema de ecuaciones simultáneas elegido es:
1) Observamos los coeficientes de una de las incógnitas con suma atención y elegiremos la pareja que nos parezca más sencilla para el propósito que perseguimos., supongamos la “x”. La manera más sencilla de lograr que tengan el mismo coeficiente es cruzarlos entre ellos, pero cuidando de que uno de los dos productos finales quede negativo. En este caso, nos conviene multiplicar la primera ecuación por 4 y la segunda por -3; el coeficiente en ambos casos tendrá un valor absoluto de 12, pero como elegimos -3 en vez de 3, la segunda ecuación quedará con coeficiente negativo en el término en x. Observa:
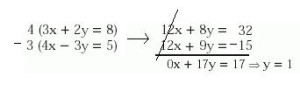2) El siguiente paso, en realidad, ya lo has observado en la imagen anterior: una vez que logras que los coeficientes de una misma incógnita sean dos números opuestos (en este caso +12 y -12), debes sumar ambas ecuaciones miembro a miembro. De este modo, los términos en “x” se reducen (por eso el método se llama método de reducción) y sólo nos queda una ecuación en “y”. La resolvemos y se llega a hallar su valor, en este caso, 1.
3) Sustituye el valor hallado de “y” (es decir el 1 en este caso), en cualquiera de las ecuaciones del sistema; quedará una ecuación sólo en “x”. Resuelve esa ecuación y hallarás la otra incógnita. Por ejemplo yo elijo hacer este procedimiento en la primera de ellas y quedará así:
3x + 2 (1) = 8
3x + 2 = 8
3 x = 6
x = 6 / 3
x = 2
4) Por último hemos de proceder a la verificación de las dos ecuaciones simultáneas. Si todo está correcto, deben verificarse las dos igualdades. Vamos paso a paso como en el ítem anterior.
Primera verificación:
a) 3 x + 2 (1) = 8
3 (2) + 2 (1) = 8
6 + 2 = 8
8 = 8
Segunda verificación:
b) 4 x – 3 (1) = 5
4 (2) – 3 (1) = 5
8 – 3 = 5
5 = 5
Cabe señalar, por último, que es posible realizar este mismo método también dividiendo coeficientes; lo que sucede es que no siempre es tan probable que todos los coeficientes de la ecuación sean múltiplos de un mismo número, o sea que puedas elegir un divisor común a todos ellos de modo que los coeficientes (preferentemente) queden enteros.
Imagen: flexi-laern
