Primero empecemos por definir que es un sistema de ecuaciones, es un conjunto de ecuaciones con varias incógnitas que normalmente son parte de un problema matemático, y la solución son aquellos valores de las incógnitas que satisfacen las ecuaciones.
Existen varios métodos para resolver sistemas de ecuaciones, el día de hoy vamos a ver los siguientes:

1.- Sustitución
2.- Igualación
3.- Reducción
4.- Método gráfico
5.- Método de Gauss
Métodos para resolver sistemas de ecuaciones
Sustitución
Este método consiste en despejar alguna de las incógnitas en una ecuación (de preferencia la incógnita que tenga menor coeficiente) y sustituir su valor en otra ecuación.
Si tuviéramos un sistema con más de dos incógnitas, la incógnita despejada se sustituye en todas las demás ecuaciones excepto en la que se despejó, y ahora se tendría un sistema pero con una ecuación y una incógnita menos, este método se puede repetir hasta llegar a la solución.
Ejemplo
Tenemos el siguiente sistema de ecuaciones
Primero despejamos una variable, en este caso la “z” de la primera ecuación ya que tiene coeficiente 1:
Sustituimos “z” en las otras dos ecuaciones:
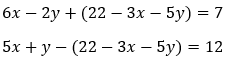
Simplificamos y despejamos otra incógnita:
Sustituimos”x” en la otra ecuación y simplificamos:
Ahora sustituimos “y” en las ecuaciones que antes despejamos
Nuestros resultados son x = 2, y = 3, z = 1
Igualación
Este método es muy parecido al de sustitución, consiste en despejar de las dos ecuaciones la misma incógnita e igualarlas, para obtener el valor de la segunda incógnita y después sustituirlo en cualquiera de las ecuaciones que despejamos.
Ejemplo
Despejamos “x”:
Igualamos y simplificamos:
Sustituimos:
Nuestros resultados son x = 3, y = 2
Reducción
Éste método es para sistemas lineales y de dos incógnitas (dos ecuaciones), consiste en utilizar productos y divisiones para hacer que en las dos ecuaciones una incógnita tenga el mismo coeficiente pero diferente signo, y luego sumar las dos ecuaciones para que así esa incógnita se elimine y nos quede una sola ecuación con una incógnita.
Ejemplo
Multiplicamos la primera ecuación por -5 y obtenemos:
Ahora sumamos las dos ecuaciones:
Sustituimos:
Nuestros resultados son x = 3, y = 2
Método gráfico
Sólo se utiliza con dos incógnitas.
Los pasos son los siguientes:
1.- Despejar “y” en las dos ecuaciones.
2.-Construir la gráfica para cada ecuación, obteniendo la tabla de valores de cada una.
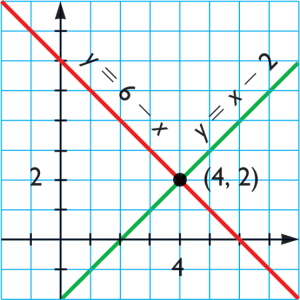
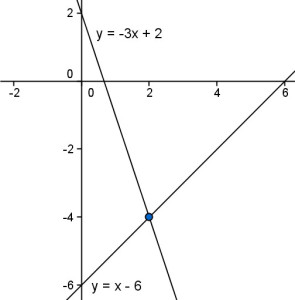
3.- Representar las dos rectas en una gráfica.
- Si las rectas se cortan, el punto de corte son los valores de “x” y “y”.
- Si son la misma recta, hay infinitas soluciones que son las coordenadas de los puntos de esa recta.
- Si las rectas son paralelas, no hay soluciones reales.
Método de Gauss
Este método consiste en convertir un sistema lineal de n ecuaciones con n incógnitas en uno en dónde la primera ecuación tiene n incógnitas, la siguiente n-1 y así sucesivamente hasta que la última tiene sólo 1 incógnita. Para resolver se parte de la última ecuación y se van sustituyendo los valores para calcular las demás incógnitas.

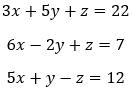

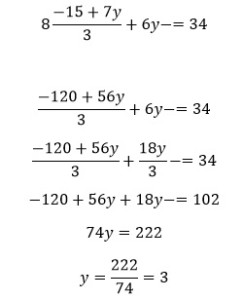
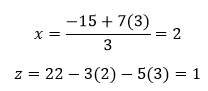
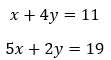
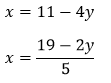
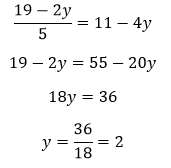
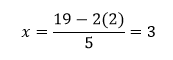
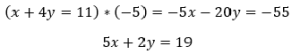
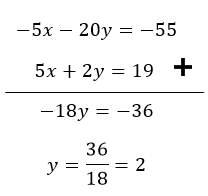
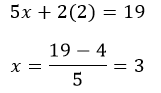


No hay respuetas