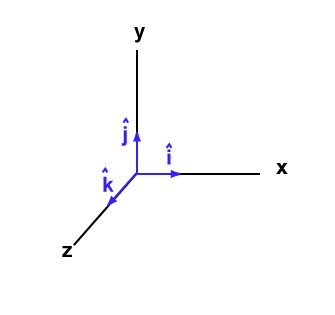
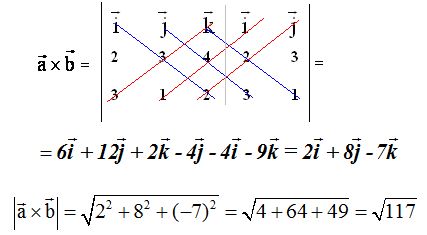
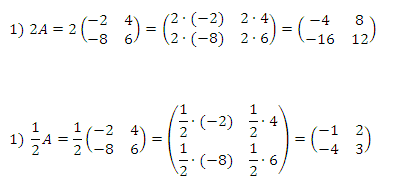Teniendo la Matriz A=
[a11 a12 a13 … a1n]
[a21 a22 a23 … a2n]
…………
[am1 am2 am3 … amn]
En lo que consiste Gauss es en llegar a una matriz, cuya diagonal principal existan unos(1), debajo de la diagonal existan ceros(0) y sobre la diagonal números.
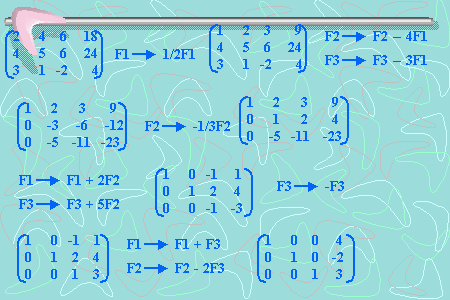
Es decir:
[a11 a12 a13] [1 b12 b13]
[a21 a22 a23] —- [0 1 b23]
[a31 a32 a33] [0 0 1]
La manera de llevar acabo es para hacer unos la diagonal ir dividiendo el numero que tenemos en la matriz entre si mismo para convertirlo en 1 y para lograr los ceros la manera es multiplicando por el numero que esta en la matriz la fila de arriba al numero a ser cero y restar ambas filas.
Veremos un ejemplo
- Teniendo la Matriz
A
[2 5]
[1 7]
Hacerla con unos en la principal diagonal, ceros debajo de esta y dejar los números que queden sobre la diagonal.
Al ver que ya tenemos un 1 en la fila debajo una manera muy simple de tener nuestro primer 1 es cambiando las filas de lugar y nuestra matriz queda:
A
[1 7]
[2 5]
La mejor recomendación para hacer Gauss es empezar por columnas, es decir, ir hacienda el ejercicio de columna en columna, por lo que toca convertir el 2 en 0, entonces multiplicamos la fila 1 por 2 y le restamos la fila 2 –importante saber que nuestra fila que fue multiplicada no cambia solo se afecta para efectos del ejercicio – y nuestra matriz nos queda:
A
[1 7]
[0 9]
Ahora como nuestra matriz tiene que tener unos en su diagonal y los de encima de esta se pueden quedar como están pasamos a transformar el 9 en 1 dividiendo la fila 2 entre 9, y así nuestra matriz A nos queda de la siguiente manera:
A
[1 7]
[0 1]
Otro ejemplo mas para ejemplificar mas la elaboracion del Gauss
- Teniendo la Matriz
A
[1 7 6]
[5 4 2]
[3 5 8]
Como ya tenemos nuestro primer uno pasamos a convertir el resto de los números de la columna en 0, por lo que multiplicamos nuestra fila 1 por 5 y por 3 respectivamente y las restamos por sus correspondientes y la matriz nos queda así:
A
[1 7 6]
[0 31 28]
[0 16 10]
Ahora pasamos a convertir a 1 el 31, dividimos la fila 2 sobre 31 y el 16 a 0 por lo que ya con el 1 que nos quedaría en nuestra fila 2, multiplicamos por 16 la fila 2 y le restamos la fila 3 y la matriz nos queda:
A
[1 7 6]
[0 1 28/31]
[0 0 138/31]
Y al final dividimos nuestra fila 3 entre 138/31 para que nos quede nuestro ultimo 1 de la diagonal y la matriz resultante ya con el Gauss completo nos queda:
A
[1 7 6]
[0 1 28/31]
[0 0 1]
De esa manera se realiza el Gauss, la recomendación siempre es buscar la manera mas fácil de resolver, si tenemos algún 1 en las filas de abajo buscar ponerlo en el fila numero 1 y a partir de ahí resolver.
Una cosa a no olvidar será que cuando multiplicamos alguna fila no la afectamos directamente en nuestra matriz simplemente se afecta para resolver el Gauss.
Ejercicios para resolver
- Aplicar Gauss y resolver las siguientes matrices
1.1:
A
[3 5]
[6 2]
1.2:
B
[2 3 10]
[1 3 7]
[2 5 8]
1.3:
X
[2 4 6]
[4 5 6]
[3 1 -2]
1.4
C
[3 12]
[5 4]