¿Cómo se calcula la superficie de un cilindro recto? Nada difícil, te invito a trabajar sobre este tema y a aprender, como siempre, en base a ejemplos. Comenzaré por definir, qué es un cilindro recto, o mejor expresado, un cilindro circular recto. Elijo tomar la definición que nos aporta wikipedia.org, que cito textualmente:
“En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, que debe ser cerrada, denominada directriz del cilindro.
Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto.”
Vayamos, ahora sí, al tema central de hoy
Superficie de un cilindro recto
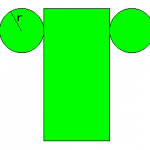
De la misma pagina citada anteriormente, tomo la imagen que ayudará a comprender la base de nuestro cálculo: el desarrollo de un cilindro recto.
Como puedes apreciar, el cuerpo en cuestión se compone de un rectángulo cuya altura es la altura del cilindro, y cuya base es lo que llamamos el perímetro de la circunferencia base, mejor dicho el perímetro del círculo que limita la circunferencia base.
Así las cosas, al igual que estudiamos en el caso de la superficie de un prisma recto, la superficie total de un cilindro se compone de la suma de su superficie lateral (en definitiva la superficie del rectángulo que señalábamos antes en el desarrollo del cilindro) más la superficie de sus bases.
La superficie de éstas últimas, será la superficie de las respectivas circunferencias base (obviamente iguales entre ellas).
Veamos cómo se realiza este cálculo, a través de un ejemplo.
¿Cómo se calcula la superficie total de un cilindro cuya altura se fija en 25 cm y cuya circunferencia base, tiene un radio de 15 cm.?
Comenzamos por calcular la superficie lateral, que como dijimos antes corresponde al área del rectángulo cuyos lados miden respectivamente: 25 cm y 2.π.15 cm (ésto último es el perímetro de la circunferencia base)
SLateral = 2.π.15 * 25 = 2355 cm2
(te recuerdo que el valor de π=3,14)
Ahora debemos calcular el área de las dos circunferencias base. Este cálculo es el siguiente:
π.r2 = π.152 = 3,14 * 225 = 706,5
Esto corresponde a una sola de las circunferencias base; te recuerdo que en el cálculo final debemos multiplicarlo por 2. De este modo, el cálculo final podría ser expresado de la siguiente manera:
ST = 2355 + 2 * 706,5 = 2355 + 1413 = 3768 cm2 .
A partir de este ejemplo, no dudo que no tendrás problemas en realizar otros cálculos similares que te sean propuestos por tu maestro o profesor. Como puedes apreciar, no reviste demasiada dificultad ya que la superficie lateral, en definitiva, es simplemente el área de un rectángulo.
Te invito a estar pendiente, entre nuestros próximos posts estará uno con ejercicios acerca de este tema y también superficies y volumen, de otros cuerpos.
Imagen: algosobre.com
