 Te invito a conocer mejor a los prismas rectos, y a trabajar específicamente sobre el tema superficie de un prisma recto. Para empezar… ¿a qué se llama un prisma recto?
Te invito a conocer mejor a los prismas rectos, y a trabajar específicamente sobre el tema superficie de un prisma recto. Para empezar… ¿a qué se llama un prisma recto?
Partimos de la definición genérica de un prisma, que tomamos desde wikipedia.org y dice textualmente:
“En geometría, un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases.”
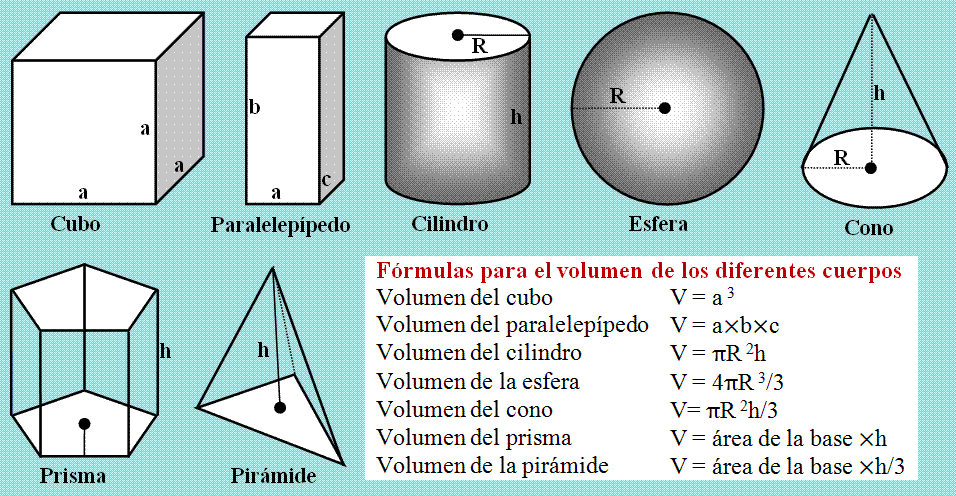
Hay muchas clases de prismas, y vale señalar que éstos se nombran en relación a qué polígono sea su base: por ejemplo, un prisma cuya base es un hexágono, es un prisma “hexagonal”.
Ahora bien… ¿qué es entonces un prisma recto?
Un prisma recto es aquel cuya bases son perpendiculares a sus caras. Mejor expresado sería decir que los planos a los que pertenecen sus bases son paralelos entre sí, y a su vez perpendiculares a los que contienen sus caras laterales.
En la figura de portada puedes observar un prisma recto de base pentagonal. Nos concentramos ahora en el tema de hoy:
Superficie de un prisma recto
Previo a esto, te invito a repasar algunos conceptos básicos en un post anterior, al que te dejo vínculo aquí mismo: Ejercicios sobre área y perímetro.
Ahora sí: debemos distinguir entre dos conceptos, la superficie total de un prisma recto y la superficie lateral de un prisma recto. Definamos cada uno de ellos:
Superficie lateral de un prisma recto, es la suma de la superficie de sus caras laterales, sin tomar en cuenta las dos bases del mismo.
Superficie total de un prisma recto, es la suma de la superficie lateral más la suma de la superficie de sus dos bases.
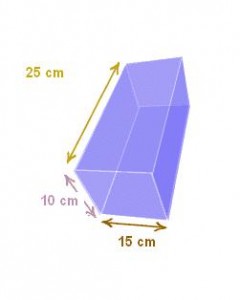
Veamos un ejemplo de cálculo. Observa atentamente el prisma de la imagen, es un prisma recto de base rectangular, dibujado en perspectiva para que puedas observar sus medidas con claridad. Como puedes apreciar, su altura es 25 cm, y las dimensiones de su base son 10 cm por 15 cm.
- Cálculo de superficie lateral
Entonces para calcular la superficie lateral:
Tenemos dos rectángulos de 25 cm por 15 cm, cuya superficie se calculará haciendo 25 cm * 15 cm = 375 cm2
Por otra parte, tenemos dos rectángulos de 25 cm por 10 cm, cuya superficie será 25 cm * 10 cm = 250 cm2
La superficie lateral, entonces es:
SL = 2 * 375 cm2 + 2 * 250 cm2 = 1250 cm2
- Cálculo de la superficie total
Como señalamos antes, la superficie total es la suma de la superficie lateral más la superficie de las bases (sumadas).
La superficie de una de las bases, es 15 cm . 10 cm = 150 cm2
Teniendo en cuenta que tiene dos bases, la suma de la superficie de éstas será: 150 * 2 = 300 cm2
Por lo tanto, la superficie total se compone con el siguiente cálculo:
STotal = 1250 cm2+ 300 cm2 = 1550 cm2
Te invito a estar pendiente: dedicaré nuestro próximo post al cálculo de volumen en un prisma recto, y posteriormente practicaremos con ejercicios interactivos acerca de superficie y volumen de prismas rectos.