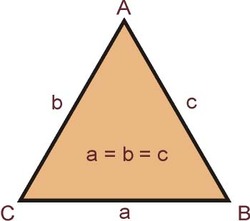
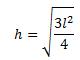Un Triángulo Equilátero es un polígono regular que tiene todos sus lados y sus ángulos iguales.
Si has podido leer los temas anteriores sobre triángulos como Clasificación de triángulos y Congruencia de triángulos, entonces ya sabes algunas de las características de estos triángulos.
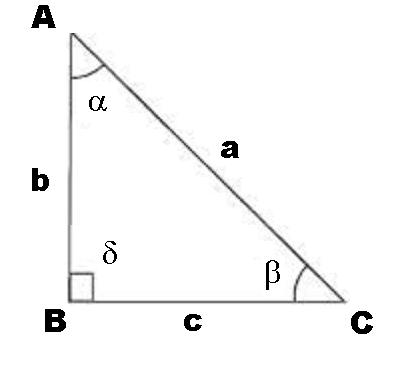
Observa la siguiente figura:
¿Qué notas?
Si tu respuesta es que todos los lados son iguales, entonces has acertado.
El nombre de “Triángulo Equilátero”, lo obtiene esta figura de la clasificación de los triángulos por sus lados, y se forma de dos palabras latinas: equis = igual y laterus = lados.
Si partiéramos de la clasificación por sus ángulos estaríamos hablando de un triángulo acutángulo, ya que se compone de tres ángulos agudos, es decir ángulos de 60 grados. Para más información sobre los ángulos y sus características Deberás revisar el siguiente tema: Clases de ángulos.
Algunas características de los triángulos equiláteros.
Es importante recordar que la suma de todos los ángulos de un Triángulo Equilátero siempre será igual a 180 grados por lo que 60 x 3 = 180.
También hay que recordar que cómo los lados y los ángulos de todo triángulo equilátero son iguales, se dice que son congruentes entre sí, ya que desde el punto de vista geométrico, decir que algo es congruente es exactamente lo mismo a decir que son iguales.
Formulas matemáticas más comunes de un Triángulo Equilátero.
A continuación te presento algunas de las formulas matemáticas más comunes para nuestra figura que es el Triángulo Equilátero, así como una breve explicación.
- Perímetro P = 3 x L Donde P = Perímetro y L= Lado. Como sabes, el perímetro es la suma de todos los lados de un triángulo, en el caso del Triángulo Equilátero, todos los lados miden lo mismo por lo que sumar 3 veces el mismo número es lo mismo que multiplicarlo.
Método para obtener la altura de un Triángulo Equilátero.
Si pudiste estudiar el tema de los Triángulos Rectángulos, pudiste notar que comentamos que el triángulo equilátero debe dividirse a la mitad, para convertirlo en dos triángulos rectángulos y de esta forma poder obtener la formula del área que hemos puesto en la parte de arriba.
¿Porqué hacer esto?
Bueno, debes recordar que el área es el espacio interno de una figura y que la Escuela de Pitágoras estudió durante mucho tiempo el triángulo rectángulo por ser este uno de los más estables, por ello, cuando se trató de estudiar triángulos diferentes, descubrieron que siempre podían usar el Teorema de Pitágoras y los triángulos Rectángulos para la obtención de los resultados requeridos. Al dividir a la mitad el triángulo equilátero podremos entonces usar el Teorema de Pitágoras estudiado en el tema de Triángulos Rectángulos.
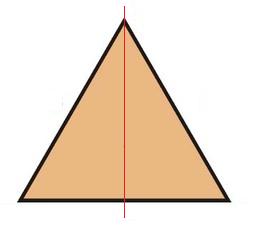
Observa la siguiente Figura:
Cómo puedes ver hemos partido la figura a la mitad y han quedado dos triángulos rectángulos. Cómo sabes, conocemos el largo de cada uno de los lados pero no conocemos el valor de la linea roja que equivale a la altura.
Denominaremos l al largo de cada uno de sus lados y h (del ingles high) a la altura.
sabemos entonces que la hipotenusa de nuestro triángulo es igual a l y que uno de los catetos es igual a l entre dos. El único dato que desconocemos es h, es decir, la altura, pero como te comenté en el tema del Triángulo Rectángulo, es posible obtener el valor de un lado partiendo del conocimiento de los otros dos.
Es posible que te cueste un poco de trabajo entender el procedimiento que mostraré a continuación debido a que haremos uso de algunos elementos de Álgebra, aún así, trataré de hacerlo de la manera más sencilla posible.
El Teorema de Pitágoras entonces dice lo siguiente:
En todo Triángulo rectángulo se cumple que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Expresado como una Formula matemática queda de la siguiente manera:
a2=b2 + c2
ahora, sustituyamos en la formula los valores y variables que hemos comentado, recuerda que a es la hipotenusa y las letras b y c son los catetos.
En álgebra, cuando hablamos de sumas, existe una regla que se conoce como conmutativa, esta regla nos dice que el orden de los sumandos no altera el resultado. Esto quiere decir que en una suma no importa en que orden estén los elementos que sumemos por lo que podemos elegir b o c para el cateto que conocemos. ¿Cuál eliges tú?
Yo elegiré el segundo por facilidad, bueno, ahora pongamos los valores en nuestra formula para que veamos como queda:
Bien, recuerda que el único dato que conocemos es la l y que debemos obtener el valor de h. Bien, observa con atención la formula anterior.
Se entiende mejor una formula cuando a una de las variables conocidas se le quitan los paréntesis. Nota que lado entre dos tiene un paréntesis que dice que todo lo que esta en ese paréntesis debe ser elevado al cuadrado, tanto lo de arriba como lo de abajo. Como sabes el cuadrado e un número es ese mismo número multiplicado por sí mismo, por lo tanto, si multiplicamos l x l tenemos que es igual a l al cuadrado, debido a que no es una constante, y al multiplicar 2 x 2 nos da igual a 4.
Reescribamos nuestra formula para ver como va quedando sin el paréntesis:
Bien, nota que ya no tenemos paréntesis pero ahora tenemos una misma variable de los dos lados de la igualdad, se le llama despeje a el proceso de “mover” de un lado a otro de una igualdad una o más variables y el proceso de despeje es en realidad muy simple, lo único que debemos hacer es esto:
tenemos una h del lado derecho y una l del lado izquierdo que queremos “mover” la h para el lado izquierdo y la l para el lado derecho.
Una igualdad no cambia si restamos o sumamos un valor de ambos lados de la igualdad, para que entiendas esto te pondré el siguiente ejemplo:
Si tienes una formula matemática como esta:
3+2 = 5
¿Dirías que es correcta?
¡Claro!, Todo el mundo sabe que 3+2 es igual a 5.
Bien, ahora, fíjate bien lo que vamos a hacer, queremos “mover” el 3 del otro lado de la igualdad o ecuación (En otro tema veremos porque se llama ecuación), para ello debemos restar el número 3 de los dos lados y te darás cuenta que aunque cambien los resultados la formula seguirá siendo correcta:
3+2-3 = 5 – 3
Nota que 3-3 = 0, así que podemos quitar los dos números 3 del lado izquierdo y nuestra ecuación queda:
2 = 5 – 3
Y por supuesto, todos sabemos que 5-3 = 2, ¿ves lo que hicimos? “despejamos” un valor de una igualdad o ecuación. Ahora hagamoslo en nuestra formula, recuerda que está de la siguiente manera:
para despejar la l2 y la h2 debemos restar a ambos lados de la ecuación l2 y h2.
Si lo hacemos suponiendo que ya sabes porque, nuestra formula queda así:
Nota que una vez que despejamos las variables, pudimos intercambiarlas, es decir “pasar” la h a la izquierda y las ls a la derecha sin que afectara nuestra igualdad.
Ya casi terminamos, nota que estamos restando quebrados. En otros temas irás aprendiendo como trabajar con variables, aquí debemos pensar por un momento que la variable esta multiplicada por uno y si revisas el tema Ejercicios con divisiones, te darás cuenta que la l2 esta dividida entre uno.
Por lo tanto, tomando el Máximo Común Divisor obtenemos el siguiente resultado:
Bien, sólo nos falta un último detalle: Quitarle a la h el cuadrado. ¿cómo crees que podemos hacer eso?
¡Muy fácil!
Sacando raíz cuadrada de ambos lados de la igualdad, y así, queda nuestro resultado de la siguiente manera:
Bien, hemos terminado, sólo nos falta tratar de lograr que se vea más estético y para ello trataremos de despejar la raíz cuadrada de la ecuación, ¿Cómo?
Nota que la l esta elevada al cuadrado y el cuatro también (su raíz es 2), mientras que el 3 no tiene raíz, dado que están multiplicadas podemos sacarle raíz a la l y al cuatro y dejar el 3 dentro de la raíz. Quedando así:
Bien, hemos terminado el largo proceso de obtener el valor de la altura de un Triángulo Equilátero.
Obtención de la formula del área de un triángulo equilátero a partir de la formula de la altura.
Ya hemos obtenido el valor de la altura del Triángulo Equilátero, lo único que nos falta es obtener la formula del triángulo rectángulo partiendo de ella.
La formula del Área del Triángulo es: 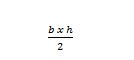
Sabemos que la base de un triángulo equilátero es lado entre dos y sustituyendo la formula de altura tenemos:
Si revisas el tema de operaciones entre variables, podrás notar que multiplicar una variable por sí misma obtendremos la variable al cuadrado y si revisas el tema de Multiplicación de Fraccionarios verás que tan sólo necesitas multiplicar los dos números de abajo por lo que la formula del área quedaría como sigue:
Bien, se que este tema quedó un poco largo. Espero no haberte cansado demasiado con él, pero se trata de que entiendas siempre el cómo y el porqué de las cosas. Sigue revisando los temas que se vayan agregando para que descubras los secretos de las matemáticas y no olvides seguir estudiando.