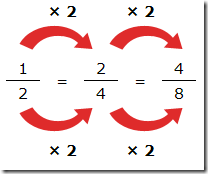
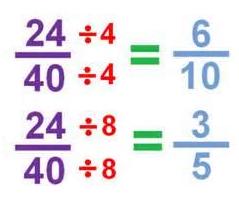 Ya hemos aprendido el concepto de fracciones equivalentes y llega el momento de practicar mediante algunos ejercicios de fracciones equivalentes. Como siempre, te planteo los mismos para que practiques y las soluciones o respuestas correctas las tienes al final de este post.
Ya hemos aprendido el concepto de fracciones equivalentes y llega el momento de practicar mediante algunos ejercicios de fracciones equivalentes. Como siempre, te planteo los mismos para que practiques y las soluciones o respuestas correctas las tienes al final de este post.
Ponte cómodo, busca un tiempo y… ¡vamos a trabajar!
Ejercicios de fracciones equivalentes
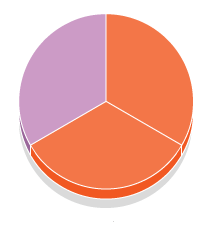
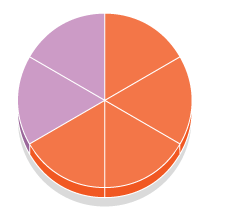
1) Las siguientes imágenes te muestran gráficos que representan fracciones equivalentes (es se nota claramente porque la superficie sombreada o coloreada es la misma en cada caso). Tu trabajo es escribir la fracción que representa cada gráfica (eso lo haces debajo de cada una de ellas) y en la fila de abajo, debes escribir el operador, es decir operación y número que te permite pasar de la primera fracción a su equivalente. Por ejemplo, si la primera fracción fuera 1/7 y la segunda fuera 3/21, el operador sería * 3, es decir “por 3”, por que para pasar de 1/7 a 3/21, debiste haber multiplicado por 3 tanto al numerador como al denominador.
 |
 |
| Fracción: |
Fracción: |
|
OPERADOR: |
|
 |
 |
| Fracción: | Fracción: |
| OPERADOR: | |
3) Escribe por lo menos 3 fracciones equivalentes para cada una de las fracciones dadas en la primera columna
| 1 /3 | |||
| 4/5 | |||
| 12/30 | |||
| 9/36 | |||
| 2/7 |
4) Simplifica las siguientes fracciones hasta lograr una fracción irreducible. En algunos casos llegarás en menos pasos que en otros (pueden sobrarte celdas que no vayas a utilizar). Ten en cuenta que en algunos casos habrá más de un divisor que puedes elegir; en la medida en que ese divisor común sea más grande, llegarás más rápidamente a obtener la fracción irreducible.
| 8/24 | ||||
| 30/42 | ||||
| 24/36 | ||||
| 20/60 | ||||
| 32/64 |
Soluciones de los ejercicios
1)
Primera fracción: 2/3 Segunda fracción: 4/ 6 Operador –> * 2 (multiplicado por 2)
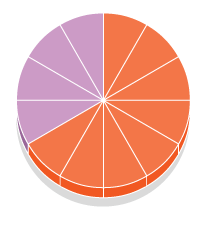
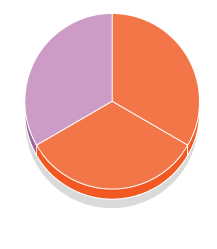
2)
Primera fracción: 8/12 Segunda fracción: 2/ 3 Operador –> / 4 (dividido por 4)
3)
Esto es un ejemplo de resolución o solución; no existe una única manera de hallar fracciones equivalentes
| 1 /3 | 2/6 | 3/9 | 4/12 |
| 4/5 | 8/10 | 40/50 | 12/15 |
| 12/30 | 6/15 | 24/60 | 3/5 |
| 9/36 | 1/4 | 90/360 | 18 / 72 |
| 2/7 | 20/70 | 6/21 | 4/14 |
4)
Esto es un ejemplo de resolución; no existe una única manera de simplificar fracciones, pero sí es única la fracción irreducible a la que debes llegar es decir, en este caso, es única la solución final.
| 8/24 | 4/12 | 1/3 | ||
| 30/42 | 15/21 | 5/7 | ||
| 24/36 | 12/18 | 6/9 | 2/3 | |
| 20/60 | 2/6 | 1/3 | ||
| 32/64 | 4/8 | 2/4 | 1/2 |
Imágenes: mathgoodies ; bbc ; sinapsi