Operaciones con fracciones

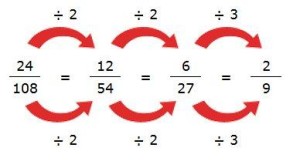
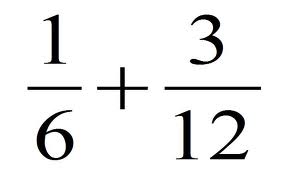Antes de ver las operaciones con fracciones repasemos brevemente que son las fracciones, una fracción es una expresión en donde una cantidad está dividida entre otra cantidad.

\begin{align} \frac{_{x}}{y} \end{align}

OPERACIONES CON FRACCIONES

Suma

Reglas generales para sumar:

1. Se simplifican las fracciones.
2. Se reducen las fracciones al mínimo común denominador (si el denominador es diferente entre las fracciones).
3. Se hacen las multiplicaciones necesarias.
4. Se suman los numeradores y se divide entre el denominador común.
5. Se reducen términos semejantes.
6. Se simplifica la fracción.

Suma de fracciones con monomios en el denominador

Ejemplo:

\begin{align}  \frac{x-2}{4} + \frac{3x+2}{6} = \end{align}
\[ \frac{3 ( x-2 )}{12} + \frac{2 ( 3x+2 )}{12} = \]
\[ \frac{3x-6}{12} + \frac{6x+4}{12} = \]
\[ \frac{3x-6+6x+4}{12} = \]
\[ \frac{9x-2}{12} \]

Suma de fracciones con polinomios en el denominador

Ejemplo:

\begin{align}  \frac{1}{a+1} + \frac{1}{a-1} = \end{align}

\[ \frac{1 ( a-1 )}{a^{2} +1^{2}} + \frac{1 ( a+1 )}{a^{2} +1^{2}} = \]

\[ \frac{a-1+a+1}{a^{2} +1^{2}} = \]

\[ \frac{2a}{a^{2} +1 \overset{}{}} \]

Resta

Reglas generales para restar fracciones:

1. Simplificar fracciones.
2. Reducir fracciones al mínimo común denominador.
3. Efectuar multiplicaciones necesarias.
4. Restar numeradores y la diferencia se divide por el mínimo común denominador.
5. Reducir términos semejantes.
6. Simplificar.

Resta de fracciones con monomios en el denominador

Ejemplo:

\begin{align} \frac{x-3}{4} – \frac{x+2}{8} = \end{align}

\[ \frac{2 ( x-3 )}{8} – \frac{x+2}{8} = \]

\[ \frac{2x-6-x-2}{8} = \]

\[ \frac{x-8}{8} \]

Resta de fracciones con polinomios en el denominador

Ejemplo:

\begin{align} \frac{1}{x-4} – \frac{1}{x-3} = \end{align}

\[ \frac{x-3}{( x-4 ) ( x-3 )} – \frac{x-4}{( x-4 ) ( x-3 )} = \]

\[ \frac{x-3-x+4}{( x-4 ) ( x-3 )} = \]

\[ \frac{1}{( x-4 ) ( x-3 )} \]

Multiplicación

Reglas generales para la multiplicación de fracciones:

1. Descomponer en factores los términos de las fracciones que se van a multiplicar.
2. Simplificar.
3. Multiplicar entre sí los numeradores y dividirlo entre la multiplicación de los denominadores.

Ejemplo:

\begin{align}  \frac{2a^{2}}{3b} \times \frac{6b^{2}}{4a} =\end{align}
\[ \frac{12a^{2} b^{2}}{12ab} \]
\[ \frac{a b}{1} \]

División 

Regla general para la división de fracciones: se multiplica el dividendo por el divisor invertido.

Ejemplo:

\begin{align} \frac{x^{2}}{3y^{2}} \div \frac{2x}{y^{3}} = \end{align}

\[ \frac{x^{2} y^{3}}{6y^{2} x} \]

\[ \frac{x y}{6} \]

Listo Ya has aprendido como realizar operaciones con fracciones, no olvides seguir practicando!