Los axiomas de geometría básica, son aquellos postulados de base, o de partida que no necesitan ni admiten demostración alguna. Por tratarse de verdades evidentes, constituyen puntos de partida a partir de los cuales se construye el resto de la teoría matemática y geométrica.
Ya abordamos una breve introducción a este concepto cuando explicamos la diferencia entere axiomas y teoremas en geometría. Te invito a re leer este post para retomar contexto y pasar introducirnos directamente en el tema de hoy.
Antes de formular los axiomas en sí mismos, vale la pena señalar que es posible que tu profesor te diga que los axiomas básicos son menos que estos (por ejemplo cinco) o que son más (porque a veces se mencionan diez). Incluso algunos profesores y maestros, realizan una clasificación de axiomas básicos distinguiendo tres tipos de axiomas, a saber: axiomas de incidencia, axiomas de orden y axiomas de congruencia.
Y…, (no te desalientes) en cursos superiores aprenderás que aún hay más, pues se habla de los axiomas de continuidad y de uno más (que no es un axioma cualquiera, créeme): el axioma de Arquímedes.
Pero hechas estas salvedades, tal como dice el título, nos quedaremos en nuestro propósito inicial, vale decir en los…
Axiomas de geometría básica
Nosotros postularemos la existencia de ocho axiomas o postulados básicos de geometría. Esto mismo hago en mis cursos presenciales y es un buen ejercicio invitar a pensar, cuál quitarías y cual agregarías -en carácter de axiomas básicos- cuando empiezas a “bucear” por los mares de la geometría.
Vamos a los axiomas uno a uno:
- Primer axioma básico: “El espacio consta de infinitos puntos, infinitas rectas e infinitos planos”.
- Segundo axioma básico: “Todo plano consta de infinitos puntos y por tanto de infinitas rectas”.
- Tercer axioma básico: “Toda recta consta de infinitos puntos”.
- Cuarto axioma básico: “Por cada punto de un plano, pasan infinitas rectas”.
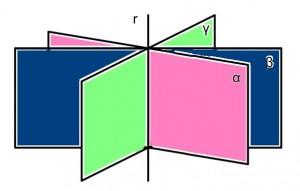
- Quinto axioma básico: “Por cada recta de un plano, pasan infinitos planos”.
- Sexto axioma básico: “Dados dos puntos, por ellos pasa una única recta”.
- Séptimo axioma básico: “Dados tres puntos no alineados, pasa por ellos un único plano”. Es pertinente señalar en este caso, que por tres puntos no alineados entendemos aquellos que no están contendidos en una misma recta.
- Octavo axioma básico: “Dados dos puntos, si pertenecen a un mismo plano, la recta que definen, también está contenida en ese mismo plano.
Veamos a continuación, algunas imágenes que ayudan a interpretar alguno de los axiomas antes señalados. Tal el caso del quinto axioma básico, que podría ser ilustrado con el siguiente dibujo:
La siguiente imagen, representa al sexto axioma básico. Vale aclarar que el tamaño de los puntos está evidentemente exagerado, tan sólo se ha dibujado así para evidenciar el concepto que sostiene el postulado, que en este caso es clarísimo: no hay otra recta que pase por esos dos puntos, que no sea la señalada.
Veamos la imagen:
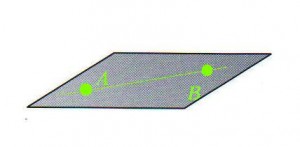Imagen: es.wikipedia
