Continuamos practicando acerca de este tema y con estos ejercicios resueltos Teorema de Pitágoras, vamos incrementando el nivel de dificultad con el fin de que ejercites tus conocimientos.
Antes hemos trabajado en resolución de triángulo con Teorema de Pitágoras, pero -tal como señalé en esa ocasión- llega el momento de pasar a otro tipo de ejercicios donde la presencia y dimensiones del triángulo rectángulo sobre el que se trabaja no siempre son tan evidentes.
Como de costumbre, te planteo algunos ejercicios dosificados por orden de dificultad y vamos aportando algunos comentarios durante el proceso de resoluición. Puedes sin duda ir midiendo tus progresos con estos…
Ejercicios resueltos Teorema de Pitágoras
- Ejercicio Nº 1
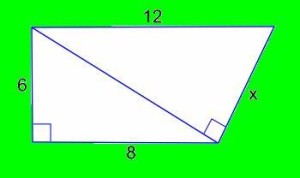
Calcula la medida del lado señalado como “x” en la siguiente figura
Un primer análisis nos permite ver que la figura se compone de dos triángulos rectángulos y que a partir de uno de ellos (el que está abajo, cuyos catetos miden 6cm y 8cm respectivamente) podemos comenzar los cálculos para llegar a responder la cuestión del problema.
Si le llamamos “a” a la hipotenusa de este triángulo, es sencillo calcular su medida a partir del enunciado directo del Teorema de Pitágoras. El planteo sería así:
a2 = 62 + 82 = 36 + 64 = 100
a = √100
a = 10
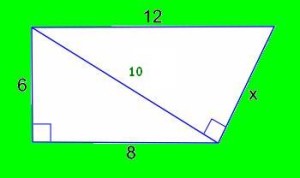
Una vez que sabemos que la hipotenusa vale 10, asumiendo que ese mismo lado es cateto del otro triángulo, podemos usar este valor más el de la hipotenusa del otro triángulo para calcular “x” que en definitiva es el cateto incógnita de este último. La figura siguiente nos ayuda en el análisis:
El planteo de la solución sería el siguiente:
122 = 102 + x2
144 = 100 + x2
x2 = 144 – 100 = 44
x = √44 = 2√11
Respuesta final: el lado x mide 2√11 cm
- Ejercicio Nº 2
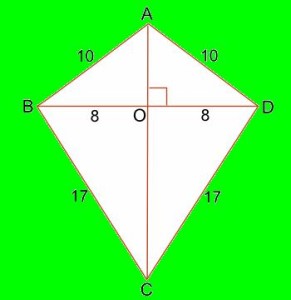
Observa la figura con atención. La pregunta es ¿Cuánto mide la diagonal mayor de la misma, es decir el segmento AC?
El análisis de esta figura nos revela que tenemos cuatro triángulos rectángulos en total (que en su conjunto componen el rombo) y tendremos que utilizar el Teorema de Pitágoras por dos veces seguidas para resolver la cuestión que se nos pide, es decir, cuál es la medida de la diagonal mayor de la figura.
Vamos por pasos; en una primera etapa éste sería el planteo a realizar sobre el triángulo AOD, llamándole “x” al segmento AO, vale decir uno de los catetos del tirángulo rectángulo en cuestión.
102 = x2 + 82
100 = x2 + 64
x2 = 100 – 64 = 36
x = √36 = 6
El segmento AO (que es parte de la diagonal mayor) mide 6 cm.
A continuación trabajaremos sobre el triángulo COD, esta vez la llamaremos “y” al segmento OC, vale decir a uno de los catetos de este segundo triángulo rectángulo que hemos definido para aplicar Teorema de Pitágoras:
172 = y2 + 82
289 = y2 + 64
y2 = 289 – 64 = 225
y = √225 = 15
Si sumamos los dos resultados parciales obtenidos, es decir 6 + 15, obtenemos la longitud de la diagonal mayor, objeto del problema inicial:
6+15=21
Repsuesta final: la diagonal AC de la figura mide 21 cm
Imagen: vaicomtudo
