Cálculo de vectores

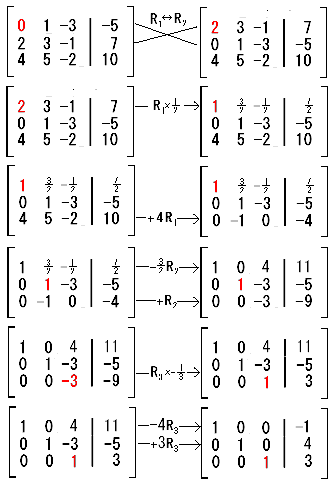
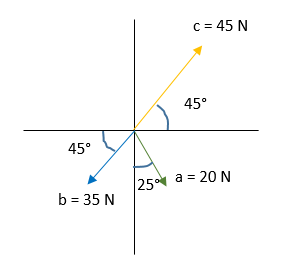
El cálculo de vectores o cálculo vectorial  es una rama de las matemáticas que estudia a los vectores y nos ayuda a solucionar problemas de la física.

Cálculo de vectores

Hay dos tipos de magnitudes físicas, las magnitudes escalares y las magnitudes vectoriales.

• Magnitudes escalares: sólo son un número, como la masa, la temperatura etc.
• Magnitudes vectoriales: tienen una cantidad, dirección y sentido, como la fuerza, el desplazamiento etc.

Un vector es un segmento en el espacio, tiene cuatro características principales:

1. Origen
2. Dirección (ángulo)
3. Sentido (signo)
4. Módulo o longitud (cantidad)

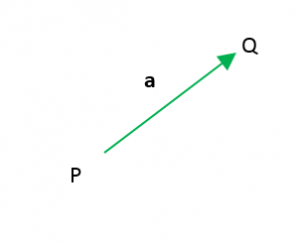
Un vector se puede representar con una flecha que indica el sentido y la longitud es la cantidad del vector:

Este vector se representa como:

\begin{align}\bar{P} \bar{Q}\end{align}

o también por el nombre del vector “a“, la longitud del segmento PQ es el módulo y se representa como:

\begin{align}| {PQ} |\end{align}

El vector unitario es aquel vector que tiene módulo 1, se suelen representar con un símbolo ^ encima.

Componentes de un vector

En dos dimensiones un vector se puede descomponer en sus componentes ax y ay.

ax = a cos α

ay= a sen α

siendo α el ángulo medido desde el eje “x” positivo en sentido opuesto a las manecillas del reloj.

a² = ax² +ay²

Operaciones con vectores

Suma de vectores

Una suma de vectores se puede hacer de dos maneras, sumando por componentes o por un método gráfico.

Suma de vectores por componentes

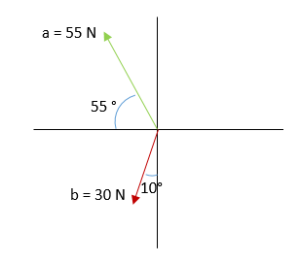
Para hacer una suma de vectores por componentes necesitamos saber las componentes en “x” y en “y” de cada vector, y  ¿cómo obtener las componentes de un vector?

a = 55 N

b = 30 N

Primero sacamos los ángulos de cada vector al eje “x” positivo en sentido opuesto al de las manecillas.

θ a =125°

θ b = 180 + 90 – 10 = 260°

Ahora sacamos las componentes en “x” multiplicando la magnitud por el coseno del ángulo al eje “x” positivo.

ax = 55N (cos 125°) = -31.55 N

bx = 30N (cos 260°) = -5.2 N

Ahora sacamos las componentes en “y” multiplicando la magnitud por el seno del ángulo al eje “x” positivo.

ay = 55N (sen 125°) = 45.05 N

by = 30N (sen 260°) = -29.54 N

**Este método tiene la ventaja de sumar o restar dos o más vectores a la vez.

Ahora sumamos las componentes en “x” y en “y”

a+b = <-36.75, 15.51>

El vector resultante tiene una magnitud de 39.89 N.

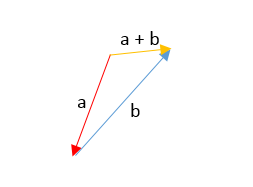
Suma de vectores por el método del paralelogramo

Una suma de vectores por este método se realiza trazando los dos vectores desde el mismo origen y formar un paralelogramo trazando líneas paralelas a los vectores, la resultante es la diagonal que se traza desde el origen.

Ejemplo:

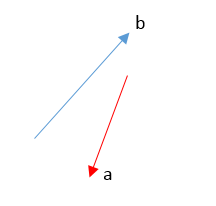
Tenemos los siguientes dos vectores:

Trazamos el vector “a” y el vector “b” desde el mismo origen y hacemos una línea paralela a cada vector para formar un paralelogramo y unimos la diagonal que va desde el origen, ese vector será la resultante:

Suma de vectores por el método cola a punta

Para hacer una suma de vectores  por este método se utilizan la regla y el transportador, existe una regla general y es la siguiente:

1. Usar la misma escala para todos los vectores
2. Trazar un vector (el orden no es importante)
3. Trazar el segundo vector, empezando desde el final del primer vector (la punta de la flecha), hay que dibujar correctamente el vector cuidando el ángulo, longitud y sentido.
4. La suma de los dos vectores es la flecha que se traza desde el principio del primer vector hasta la punta del segundo.

NOTA: este método se puede usar con más vectores.

Ejemplo:

Tenemos los siguientes dos vectores:

Ahora trazamos el vector “a” y en la punta de la flecha trazamos el vector “b”, unimos el inicio de a con la punta de b y tendremos nuestro vector resultante:

Resta de vectores

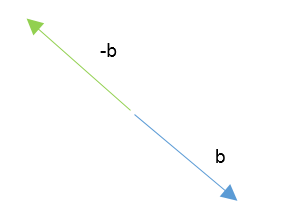
La diferencia de  vectores a y b será otro vector c = a – b que se puede expresar como una suma, la suma de a y el opuesto de b:

\begin{align}\overset{}{} \overset{\rightarrow}{c} = \overset{\rightarrow}{a} -\overset{\rightarrow}{b} = \overset{\rightarrow}{a} + \left( -\overset{\rightarrow}{b} \right)\end{align}

el opuesto del vector b tiene la misma magnitud y la misma dirección pero sentido opuesto.

Opuesto de un vector

Como vimos en la fórmula, convertimos la resta en una suma, entonces tenemos que representar el opuesto del segundo vector y lo sumamos con el primero y ya podemos resolver la suma con cualquiera de los métodos para sumar vistos anteriormente.

Multiplicación de vectores

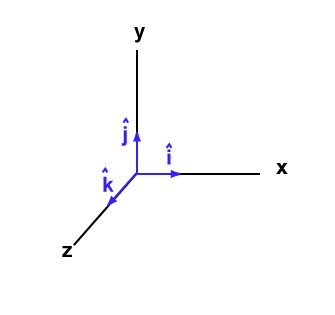
El producto de vectores u y v es otro vector, su dirección es perpendicular a los dos vectores, su sentido está dado por la regla de la mano derecha, su magnitud es:

\begin{align}\left| \overset{\rightarrow}{u} \right| \left| \overset{}{} \overset{\rightarrow}{v} \right| {sen } \alpha\end{align}

α es el ángulo entre los dos vectores.

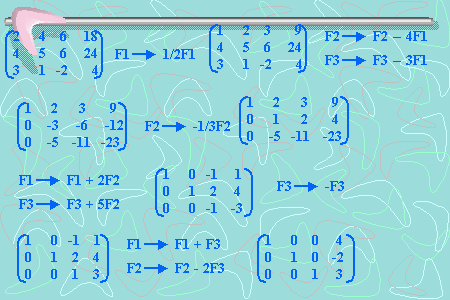
El producto de vectores se puede expresar con determinantes:

\begin{align}\overset{\rightarrow}{u} \times \overset{\rightarrow}{v} =
\left(\begin{array}{ccc}
\overset{\rightarrow}{i} & \overset{\rightarrow}{j} &
\overset{\rightarrow}{k}\\
u_{1} & u_{2} & u_{3}\\
v_{1} & v_{2} & v_{3}
\end{array}\right) = \left(\begin{array}{cc}
u_{2} & u_{3}\\
v_{2} & v_{3}
\end{array}\right) \overset{\rightarrow}{i} – \left(\begin{array}{cc}
u_{1} & u_{3}\\
v_{1} & v_{3}
\end{array}\right) \overset{\rightarrow}{j} + \left(\begin{array}{cc}
u_{1} & u_{2}\\
v_{1} & v_{2}
\end{array}\right) \overset{\rightarrow}{k}\end{align}

ó

\begin{align}\overset{}{} \overset{\rightarrow}{u} \times \overset{\rightarrow}{v} = (
u_{2} v_{3} -v_{2} u_{3} ) i- ( u_{1} v_{3} -v_{1} u_{3} ) j+ ( u_{1} v_{2}
-v_{1} u_{2} ) k\end{align}

Ejemplo