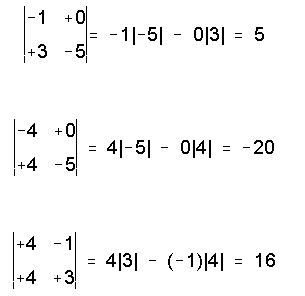El producto punto o producto escalar entre dos vectores es muy sencillo de obtener, si deseas repasar más el tema te recomiendo que leas el siguiente artículo “Producto punto”
Ejercicios de producto punto
Te pongo los siguientes ejercicios para que intentes resolverlos y al final te muestro la solución para que compares tus resultados:
1.- \begin{align} \vec{u} = [1 ,1,1] \end{align}
\begin{align} \vec{v} = [ 2 ,2,2 ] \end{align}
2.- \begin{align} \vec{u} = [ 3 ,7,5 ] \end{align}
\begin{align} \vec{v} = [2 ,-3,1] \end{align}
3.- \begin{align} \vec{u} = [ 12 ,4,6 ] \end{align}
\begin{align} \vec{v} = [ 8 ,9,-1 ] \end{align}
4.- \begin{align} \vec{u} = [ 5 ,-2,10 ] \end{align}
\begin{align} \vec{v} = [ 7 ,4,4 ] \end{align}
5.-\begin{align} \vec{u} = [ 1 ,-6,3 ] \end{align}
\begin{align} \vec{v} = [ -2 ,-3,-4 ] \end{align}
6.- \begin{align} \vec{u} = [ 15 ,3,1 ] \end{align}
\begin{align} \vec{v} = [-15 ,-3,-1 ] \end{align}
7.-\begin{align} \vec{u} = [ 12 ,2,6 ] \end{align}
\begin{align} \vec{v} = [1 ,5,7 ] \end{align}
Ejercicios resueltos de producto punto
1.- \begin{align} \vec{u} \cdot \vec{v} = 1 \cdot 2+1 \cdot 2 +1 \cdot 2 = 6\end{align}
2.- \begin{align} \vec{u} \cdot \vec{v} = 3 \cdot 2+7 \cdot -3 +5\cdot 1 = -10\end{align}
3.- \begin{align} \vec{u} \cdot \vec{v} = 12\cdot 8 +4\cdot 9 +6 \cdot -1 = 126\end{align}
4.- \begin{align} \vec{u} \cdot \vec{v} = 5\cdot 7 +-2\cdot 4 +10 \cdot 4 = 67\end{align}
5.- \begin{align} \vec{u} \cdot \vec{v} = 1\cdot -2+-6\cdot -3 +3 \cdot -4 = 4\end{align}
6.- \begin{align} \vec{u} = \sqrt{ 15^{2} + 3^{2} +1^{2}} = 15.33\end{align}
\begin{align} \vec{v} = \sqrt{ -15^{2} + -3^{2} +-1^{2}} = 15.33 \end{align}
\begin{align} \cos \alpha = \frac{15\cdot -15 +3 \cdot -3+1 \cdot-1}{\sqrt{ 15^{2} + 3^{2} +1^{2}} \cdot \sqrt{ -15^{2} + -3^{2} +-1^{2}}} = = -.999\end{align}
\begin{align}\vec{u} \cdot \vec{v} = | 15.33| \cdot | 15.33 | \cdot -.999 = -235 \end{align}
7.- \begin{align} \vec{u} = \sqrt{ 12^{2} + 2^{2} +6^{2}} = 13.56\end{align}
\begin{align} \vec{v} = \sqrt{ 1^{2} + -5^{2} +7^{2}} = 75 \end{align}
\begin{align} \cos \alpha = \frac{12\cdot 1 +2 \cdot 5+6 \cdot7}{\sqrt{ 12^{2} + 2^{2} +6^{2}} \cdot \sqrt{ 1^{2} + -5^{2} +7^{2}}} = = -.0629\end{align}
\begin{align}\vec{u} \cdot \vec{v} = | 13.56| \cdot |75 | \cdot -.0629= -64 \end{align}
