Cómo resolver ecuaciones con fracciones es muy similar a cómo resolver ecuaciones con enteros, pero debes tener en cuenta una serie de reglas básicas que te permitirán manejar las fracciones sin miedo. Una ecuación es fraccionaria si al menos uno de sus términos tiene denominador, es decir, que tengas aunque sea una incógnita dividida entre un número. 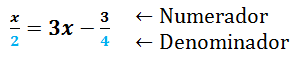 Cómo resolver ecuaciones con fracciones se vuelve mucho más sencillo si suprimes los denominadores y la conviertes en una ecuación con enteros. Te podrás preguntar cómo se convierte esto, pero es muy sencillo: Lo primero que tienes que hacer para saber cómo resolver ecuaciones con fracciones es suprimir los denominadores, o sea encontrar el mínimo común múltiplo (m.c.m.) de todos los denominadores que tengas en tu ecuación. (El m.c.m. de dos o más expresiones algebraicas es la que tenga el coeficiente numérico más pequeño y el exponente menor, que se puede dividir exactamente entre cada una de las expresiones dadas)
Cómo resolver ecuaciones con fracciones se vuelve mucho más sencillo si suprimes los denominadores y la conviertes en una ecuación con enteros. Te podrás preguntar cómo se convierte esto, pero es muy sencillo: Lo primero que tienes que hacer para saber cómo resolver ecuaciones con fracciones es suprimir los denominadores, o sea encontrar el mínimo común múltiplo (m.c.m.) de todos los denominadores que tengas en tu ecuación. (El m.c.m. de dos o más expresiones algebraicas es la que tenga el coeficiente numérico más pequeño y el exponente menor, que se puede dividir exactamente entre cada una de las expresiones dadas) 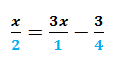 En el ejemplo de cómo resolver ecuaciones con fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4 se puede dividir exactamente entre 2, entre 1 y entre 4, mira
En el ejemplo de cómo resolver ecuaciones con fracciones, el m.c.m. entre los denominadores (que son 2, 1 y 4) es 4 porque 4 se puede dividir exactamente entre 2, entre 1 y entre 4, mira 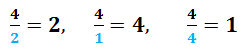 Ahora bien, una vez encontrado el m.c.m. de tu expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una ecuación no se altera si haces las mismas operaciones de los dos lados del signo igual.)
Ahora bien, una vez encontrado el m.c.m. de tu expresión, lo que tienes que hacer para continuar en el cómo resolver ecuaciones con fracciones es multiplicar toda la ecuación por ese número. (Recuerda que una ecuación no se altera si haces las mismas operaciones de los dos lados del signo igual.) 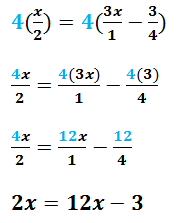 Y listo, lo que sigue para saber cómo resolver ecuaciones con fracciones es encontrar el valor de la incógnita de la misma forma que resolverías una ecuación con enteros: reduces términos semejantes, despejas la incógnita y resuelves.
Y listo, lo que sigue para saber cómo resolver ecuaciones con fracciones es encontrar el valor de la incógnita de la misma forma que resolverías una ecuación con enteros: reduces términos semejantes, despejas la incógnita y resuelves. 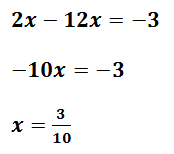 En caso de que te encuentres con un numerador con un polinomio (que tenga más de un término, o sea que tenga alguna suma o resta en la parte de arriba de la fraccion) no cambia nada en el cómo se resuelven ecuaciones con fracciones: se realizan los mismos pasos; ahora verás.
En caso de que te encuentres con un numerador con un polinomio (que tenga más de un término, o sea que tenga alguna suma o resta en la parte de arriba de la fraccion) no cambia nada en el cómo se resuelven ecuaciones con fracciones: se realizan los mismos pasos; ahora verás. 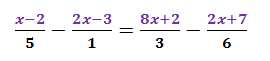 En el ejemplo puedes observar que todos los numeradores son más de un término, pero eso no afecta en nada, tu debes encontrar el m.c.m. de los denominadores: entre los números 1,5, 3 y 6 su m.c.m. es 30, así que multiplicamos toda la ecuación por 30
En el ejemplo puedes observar que todos los numeradores son más de un término, pero eso no afecta en nada, tu debes encontrar el m.c.m. de los denominadores: entre los números 1,5, 3 y 6 su m.c.m. es 30, así que multiplicamos toda la ecuación por 30 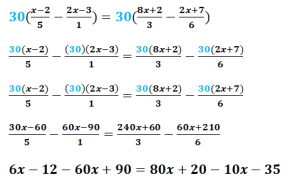 Y al eliminar todos los denominadores, entonces resolvemos la ecuación de la misma forma como se resuelve una con enteros: despejando la incógnita.
Y al eliminar todos los denominadores, entonces resolvemos la ecuación de la misma forma como se resuelve una con enteros: despejando la incógnita. ![]()
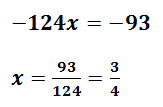 En estos dos ejemplos es muy sencillo saber cuál es el m.c.m., pero para el caso de que te encuentres con denominadores más complejos, te explico una manera sencilla de encontrar el m.c.m. de cualquier combinación de números, siempre y cuando sean monomios.
En estos dos ejemplos es muy sencillo saber cuál es el m.c.m., pero para el caso de que te encuentres con denominadores más complejos, te explico una manera sencilla de encontrar el m.c.m. de cualquier combinación de números, siempre y cuando sean monomios.
- Se descomponen los coeficientes de cada número dado en factores primos (o sea los número que solo pueden dividirse entre sí mismos y entre 1, como 1, 2, 3, 5, 7, 11, 13,17,19,23..) elevados a un cierto exponente.
- Tomamos todas las literales que existen en al menos un término dado con el mayor exponente encontrado.
- Tomamos todos los números primos encontrados con el exponente mayor encontrado.
Mira el ejemplo: