Problemas resueltos aplicando trigonometría

Los problemas resueltos aplicando trigonometría son el paso siguiente a los ejercicios de trignometría básica, sobre los que trabajaste antes.

Ten en cuenta que a veces, algo así como por “inercia” en  este tipo de ejercicios uno tiene la tendencia de resolver completamente un triángulo una vez que lo detecta, pero lo cierto es que sólo debes remitirte a la pregunta en cuestión y realizar los cálculos necesarios para la obtención de esa respuesta. Rara vez se te pide que resuelvas la totalidad del triángulo…

Me explicaré mejor, como siempre, con un ejemplo que iremos resolviendo y explicando paso a paso. He aquí el primero de los

Problemas resueltos aplicando trigonometría

• Primer problema

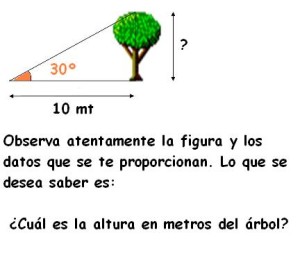
Observa con atención lo que te mencionaba al principio: está claro cuál es el triángulo sobre el que trabajarás… pero ten en cuenta que sólo se te pide hallar la altura del árbol, que -en este caso- es el cateto opuesto al ángulo señalado en color naranja, que mide 30º.

Como el otro dato que te brinda el problema es el cateto adyacente al mismo ángulo, al momento de buscar cuál de las funciones trigonométricas que conoces es la que nos conviene utilizar, rápidamente verás que es la tangente ya que relaciona precisamente ambos catetos entre sí.

Este será el planteo a realizar:

• Segundo problema

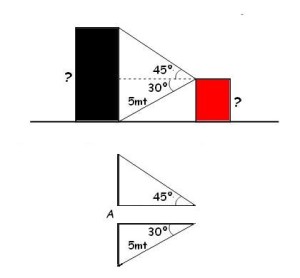
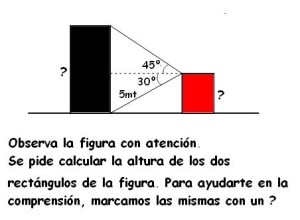 Para un correcto análisis del problema, hemos de centrar atención en las medidas o datos que nos aportan entre medio de los dos rectángulos en cuestión. De allí podemos extractar o apartar dos triángulos, que nos servirán para hacer los cálculos. Observa a qué me refiero:

Comienzo por el triángulo de abajo, donde utilizaré la fórmula del sen 30º, que relaciona la hipotenusa del triángulo (valor que conocemos porque vale 5 mt) y el cateto opuesto (medida que queremos conocer y que corresponde a la altura del rectángulo rojo).

El cálculo quedaría expresado así:

sen 30º = cat.op / hipotenusa

         0,5 = cat.op / 5

0,5 * 5   = cat op

2,5 mt = cat op

Sigo trabajando sobre el mismo triángulo, pero esta vez querremos hallar el cateto adyacente a 30º, porque tal como se ve, es también la medida del adyacente en el triángulo de arriba, es decir el que tiene ángulo 45º.

Para eso utilizo la fórmula de coseno:

cos 30º= cat.ady/hip

0,86  = cat ady / 5

0,86 * 5 = cat ady

4,3 tm  = cat. ady

Por último, es el momento de utilizar esta medida, para que a través de la función trigonométrica tangente (en este caso de 45º) sea posible hallar el segmento restante que nos permitirá (sumado al anterior) hallar la altura del rectángulo de color negro.

Los cálculos quedan planteados de la siguiente manera:

tg 45º= cat.op / cat ady

          1 = cat.op / 4,3

1 * 4.3 = cat.op

4,3 mt = cat op

Así las cosas, ya estás listo para poder aportar la respuesta final a la pregunta del problema:

Altura del rectángulo color rojo:  2,5 mt

Altura del rectángulo color negro: 2,5 mt + 4,3 mt = 6,8 mt

Conclusiones

Como has podido apreciar, dos momentos son cruciales a la hora de resolver este tipo de problemas con trigonometría: el primero es lograr aislar y re dibujar uno o más triángulos que necesariamente tienen que contar con algunas medidas (ángulos o lados) de donde se pueda partir.

El segundo es elegir cuál de las razones o funciones trigonométricas será la apropiada en cada caso.

Por último, es clave rearmar los resultados de los cálculos para responder la incógnita concreta del problema.