Teorema de los cosenos

El teorema de los cosenos se puede aplicar de forma directa para calcular las partes restantes de un triángulo oblicuo (Triángulo que no contiene un ángulo recto), cuando se tiene cualquiera de los dos siguientes:

• Dos lados y el ángulo entre ellos
• Los tres lados

El teorema de los cosenos es el siguiente:

Si ABC es un triángulo, entonces: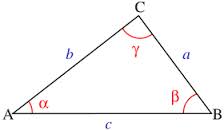

1. a² = b² + c² – 2bc cos α
2. b² = a² + c² – 2ac cos β
3. c² = a² + b² – 2ab cos ϒ

Teorema de los cosenos

En vez de memorizar las tres fórmulas podrías mejor recordar la siguiente oración del teorema de los cosenos que se puede aplicar en todos los casos :

“El cuadrado de la longitud de cualquier lado de un triángulo es igual a la suma de los cuadrados de las longitudes de los otros dos lados, menos el doble producto de las longitudes de los dos lados por el coseno del ángulo que forman entre ellos”.

 Ejemplos del teorema de los cosenos

1.  Determinar el otro lados del triángulo  si a=6, c=8 y β=70°

Calculamos el lado b con la fórmula  b² = a² + c² – 2ac cos β

b² = (6)² +(8)² – 2(6)(8) cos (70)

b² = 36+64 – 96 cos (70)

b² = 100 – 96 cos (70)

b² ≈ 67

b≈ 8.1

2. Determinar los ángulos si los lados del triángulo son a = 95, b = 70 y c = 35.

a² = b² + c² – 2bc cos α

cos α = (a² – b² – c² )/-2bc

cos α = (95² – 70² – 35² )/-2(70)(35)

cos α = 2900/4900

cos α = -.591836

α  ≈ 126 °

b² = a² + c² – 2ac cos β

cos β = (b² – a² – c² )/-2ac

cos β = (70² – 95² – 35² )/-2(95)(35)

cos β = -5350/-6650

cos β = .8045

β  ≈ 37 °

c² = a² + b² – 2ab cos ϒ

cos γ = (c² – a² – b² )/-2ab

cos γ = (35² – 95² – 70² )/-2(95)(70)

cos γ = -12700/-13300

cos γ = .9548

γ  ≈ 17 °

Comprobando 17 + 37 + 126 = 180, los ángulos internos de un triángulo siempre suman 180.

Ahora que ya conoces el Teorema de los cosenos y como se usa ya puedes practicar!